Neural Network-Assisted Nonlinear Multiview Component Analysis: Identifiability and Algorithm

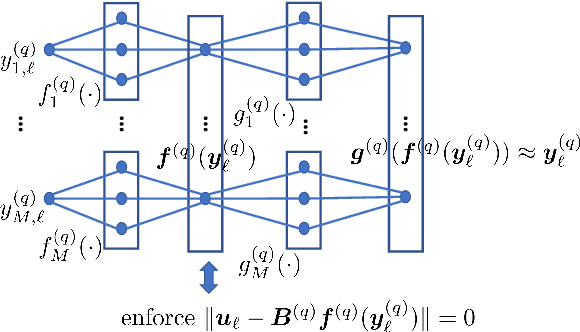
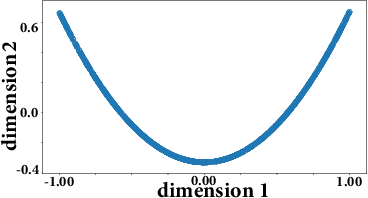
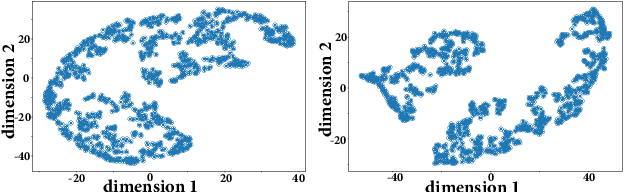
Multiview analysis aims at extracting shared latent components from data samples that are acquired in different domains, e.g., image, text, and audio. Classic multiview analysis, e.g., Canonical Correlation Analysis (CCA), tackles this problem via matching the linearly transformed views in a certain latent domain. More recently, powerful nonlinear learning tools such as kernel methods and neural networks are utilized for enhancing the classic CCA. However, unlike linear CCA whose theoretical aspects are clearly understood, nonlinear CCA approaches are largely intuition-driven. In particular, it is unclear under what conditions the shared latent components across the veiws can be identified---while identifiability plays an essential role in many applications. In this work, we revisit nonlinear multiview analysis and address both the theoretical and computational aspects. We take a nonlinear multiview mixture learning viewpoint, which is a natural extension of the classic generative models for linear CCA. From there, we derive a nonlinear multiview analysis criteron. We show that minimizing this criterion leads to identification of the latent shared components up to certain ambiguities, under reasonable conditions. Our derivation and formulation also offer new insights and interpretations to existing deep neural network-based CCA formulations. On the computation side, we propose an effective algorithm with simple and scalable update rules. A series of simulations and real-data experiments corroborate our theoretical analysis.