Latent Correlation-Based Multiview Learning and Self-Supervision: A Unifying Perspective
Paper and Code
Jun 17, 2021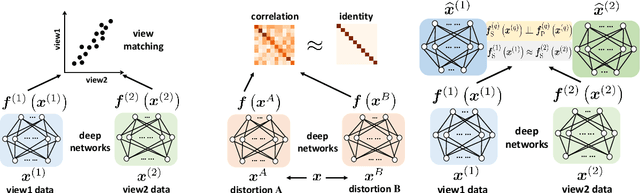
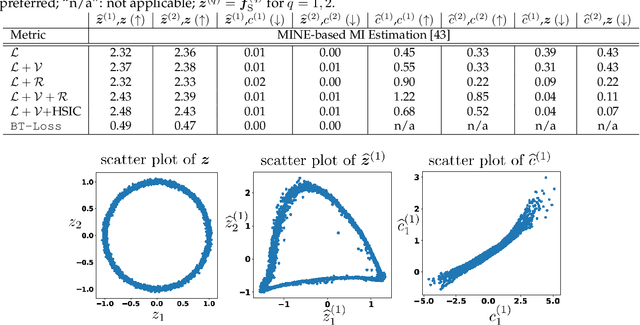
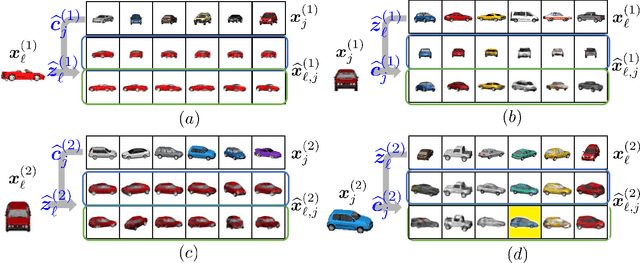
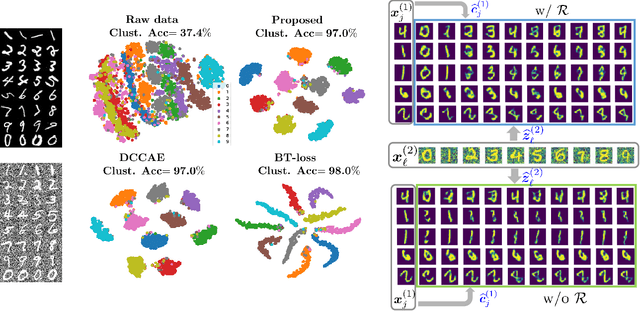
Multiple views of data, both naturally acquired (e.g., image and audio) and artificially produced (e.g., via adding different noise to data samples), have proven useful in enhancing representation learning. Natural views are often handled by multiview analysis tools, e.g., (deep) canonical correlation analysis [(D)CCA], while the artificial ones are frequently used in self-supervised learning (SSL) paradigms, e.g., SimCLR and Barlow Twins. Both types of approaches often involve learning neural feature extractors such that the embeddings of data exhibit high cross-view correlations. Although intuitive, the effectiveness of correlation-based neural embedding is only empirically validated. This work puts forth a theory-backed framework for unsupervised multiview learning. Our development starts with proposing a multiview model, where each view is a nonlinear mixture of shared and private components. Consequently, the learning problem boils down to shared/private component identification and disentanglement. Under this model, latent correlation maximization is shown to guarantee the extraction of the shared components across views (up to certain ambiguities). In addition, the private information in each view can be provably disentangled from the shared using proper regularization design. The method is tested on a series of tasks, e.g., downstream clustering, which all show promising performance. Our development also provides a unifying perspective for understanding various DCCA and SSL schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge