Scale-Robust Timely Asynchronous Decentralized Learning

We consider an asynchronous decentralized learning system, which consists of a network of connected devices trying to learn a machine learning model without any centralized parameter server. The users in the network have their own local training data, which is used for learning across all the nodes in the network. The learning method consists of two processes, evolving simultaneously without any necessary synchronization. The first process is the model update, where the users update their local model via a fixed number of stochastic gradient descent steps. The second process is model mixing, where the users communicate with each other via randomized gossiping to exchange their models and average them to reach consensus. In this work, we investigate the staleness criteria for such a system, which is a sufficient condition for convergence of individual user models. We show that for network scaling, i.e., when the number of user devices $n$ is very large, if the gossip capacity of individual users scales as $\Omega(\log n)$, we can guarantee the convergence of user models in finite time. Furthermore, we show that the bounded staleness can only be guaranteed by any distributed opportunistic scheme by $\Omega(n)$ scaling.

Age of Information in Gossip Networks: A Friendly Introduction and Literature Survey

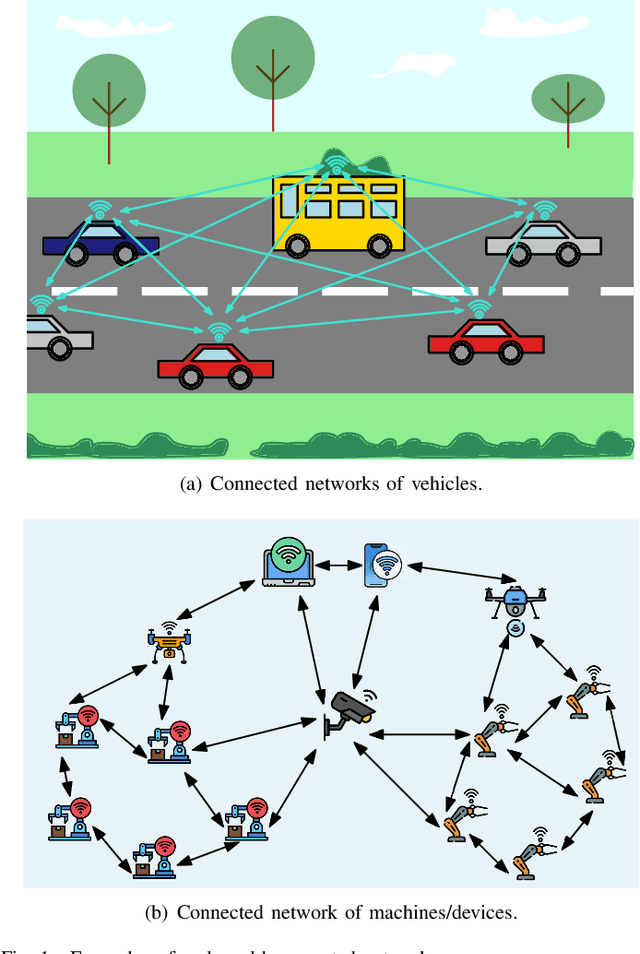
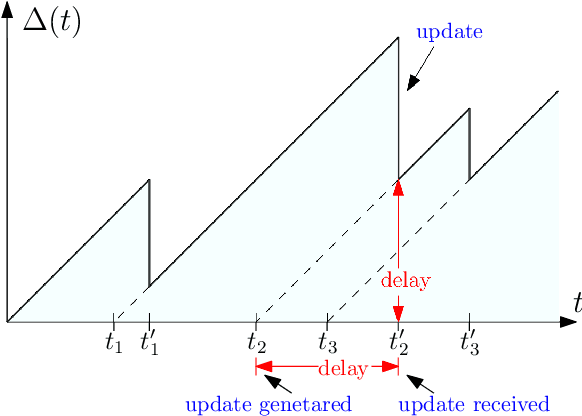
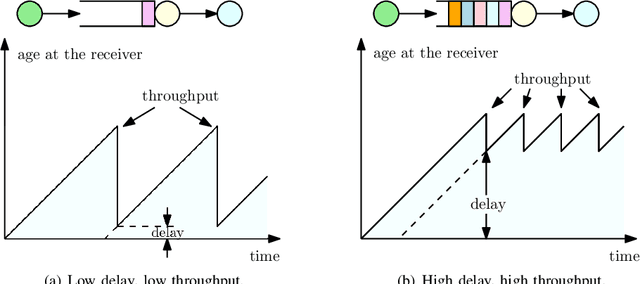
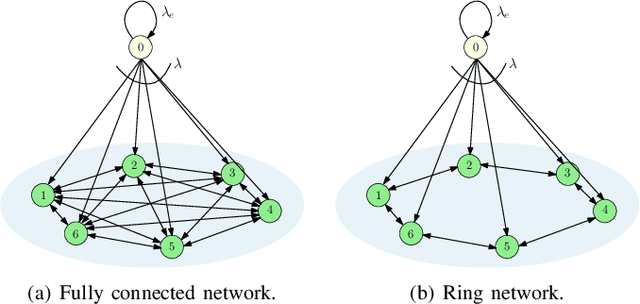
Gossiping is a communication mechanism, used for fast information dissemination in a network, where each node of the network randomly shares its information with the neighboring nodes. To characterize the notion of fastness in the context of gossip networks, age of information (AoI) is used as a timeliness metric. In this article, we summarize the recent works related to timely gossiping in a network. We start with the introduction of randomized gossip algorithms as an epidemic algorithm for database maintenance, and how the gossiping literature was later developed in the context of rumor spreading, message passing and distributed mean estimation. Then, we motivate the need for timely gossiping in applications such as source tracking and decentralized learning. We evaluate timeliness scaling of gossiping in various network topologies, such as, fully connected, ring, grid, generalized ring, hierarchical, and sparse asymmetric networks. We discuss age-aware gossiping and the higher order moments of the age process. We also consider different variations of gossiping in networks, such as, file slicing and network coding, reliable and unreliable sources, information mutation, different adversarial actions in gossiping, and energy harvesting sensors. Finally, we conclude this article with a few open problems and future directions in timely gossiping.

A Learning Based Scheme for Fair Timeliness in Sparse Gossip Networks

We consider a gossip network, consisting of $n$ nodes, which tracks the information at a source. The source updates its information with a Poisson arrival process and also sends updates to the nodes in the network. The nodes themselves can exchange information among themselves to become as timely as possible. However, the network structure is sparse and irregular, i.e., not every node is connected to every other node in the network, rather, the order of connectivity is low, and varies across different nodes. This asymmetry of the network implies that the nodes in the network do not perform equally in terms of timelines. Due to the gossiping nature of the network, some nodes are able to track the source very timely, whereas, some nodes fall behind versions quite often. In this work, we investigate how the rate-constrained source should distribute its update rate across the network to maintain fairness regarding timeliness, i.e., the overall worst case performance of the network can be minimized. Due to the continuous search space for optimum rate allocation, we formulate this problem as a continuum-armed bandit problem and employ Gaussian process based Bayesian optimization to meet a trade-off between exploration and exploitation sequentially.

Timely Asynchronous Hierarchical Federated Learning: Age of Convergence

We consider an asynchronous hierarchical federated learning (AHFL) setting with a client-edge-cloud framework. The clients exchange the trained parameters with their corresponding edge servers, which update the locally aggregated model. This model is then transmitted to all the clients in the local cluster. The edge servers communicate to the central cloud server for global model aggregation. The goal of each client is to converge to the global model, while maintaining timeliness of the clients, i.e., having optimum training iteration time. We investigate the convergence criteria for such a system with dense clusters. Our analysis shows that for a system of $n$ clients with fixed average timeliness, the convergence in finite time is probabilistically guaranteed, if the nodes are divided into $O(1)$ number of clusters, that is, if the system is built as a sparse set of edge servers with dense client bases each.

Age-Aware Gossiping in Network Topologies

We consider a fully-connected wireless gossip network which consists of a source and $n$ receiver nodes. The source updates itself with a Poisson process and also sends updates to the nodes as Poisson arrivals. Upon receiving the updates, the nodes update their knowledge about the source. The nodes gossip the data among themselves in the form of Poisson arrivals to disperse their knowledge about the source. The total gossiping rate is bounded by a constraint. The goal of the network is to be as timely as possible with the source. We propose a scheme which we coin \emph{age sense updating multiple access in networks (ASUMAN)}, which is a distributed opportunistic gossiping scheme, where after each time the source updates itself, each node waits for a time proportional to its current age and broadcasts a signal to the other nodes of the network. This allows the nodes in the network which have higher age to remain silent and only the low-age nodes to gossip, thus utilizing a significant portion of the constrained total gossip rate. We calculate the average age for a typical node in such a network with symmetric settings, and show that the theoretical upper bound on the age scales as $O(1)$. ASUMAN, with an average age of $O(1)$, offers significant gains compared to a system where the nodes just gossip blindly with a fixed update rate, in which case the age scales as $O(\log n)$. Further, we analyzed the performance of ASUMAN for fractional, finitely connected, sublinear and hierarchical cluster networks. Finally, we show that the $O(1)$ age scaling can be extended to asymmetric settings as well. We give an example of power law arrivals, where nodes' ages scale differently but follow the $O(1)$ bound.

Timely Opportunistic Gossiping in Dense Networks

We consider gossiping in a fully-connected wireless network consisting of $n$ nodes. The network receives Poisson updates from a source, which generates new information. The nodes gossip their available information with the neighboring nodes to maintain network timeliness. In this work, we propose two gossiping schemes, one semi-distributed and the other one fully-distributed. In the semi-distributed scheme, the freshest nodes use pilot signals to interact with the network and gossip with the full available update rate $B$. In the fully-distributed scheme, each node gossips for a fixed amount of time duration with the full update rate $B$. Both schemes achieve $O(1)$ age scaling, and the semi-distributed scheme has the best age performance for any symmetric randomized gossiping policy. We compare the results with the recently proposed ASUMAN scheme, which also gives $O(1)$ age performance, but the nodes need to be age-aware.

ASUMAN: Age Sense Updating Multiple Access in Networks

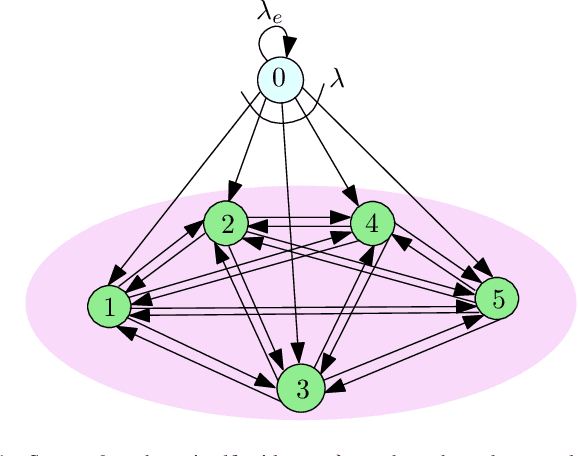
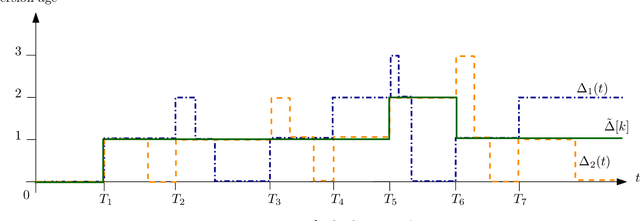
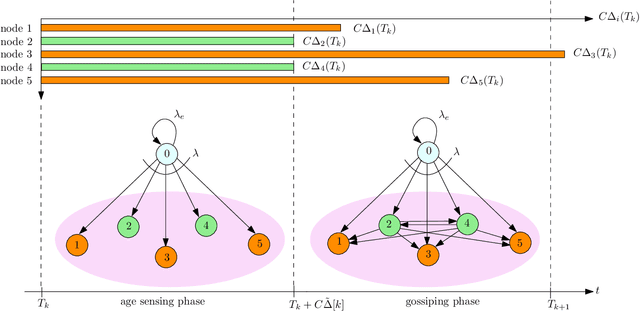
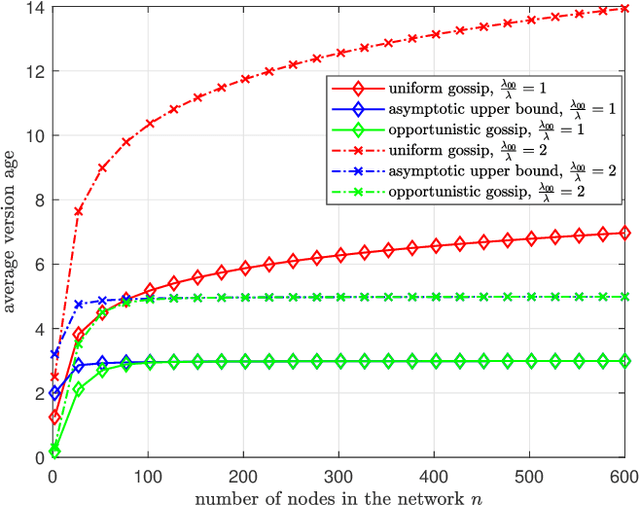
We consider a fully-connected wireless gossip network which consists of a source and $n$ receiver nodes. The source updates itself with a Poisson process and also sends updates to the nodes as Poisson arrivals. Upon receiving the updates, the nodes update their knowledge about the source. The nodes gossip the data among themselves in the form of Poisson arrivals to disperse their knowledge about the source. The total gossiping rate is bounded by a constraint. The goal of the network is to be as timely as possible with the source. In this work, we propose ASUMAN, a distributed opportunistic gossiping scheme, where after each time the source updates itself, each node waits for a time proportional to its current age and broadcasts a signal to the other nodes of the network. This allows the nodes in the network which have higher age to remain silent and only the low-age nodes to gossip, thus utilizing a significant portion of the constrained total gossip rate. We calculate the average age for a typical node in such a network with symmetric settings and show that the theoretical upper bound on the age scales as $O(1)$. ASUMAN, with an average age of $O(1)$, offers significant gains compared to a system where the nodes just gossip blindly with a fixed update rate in which case the age scales as $O(\log n)$.