ASUMAN: Age Sense Updating Multiple Access in Networks
Paper and Code
Jul 14, 2022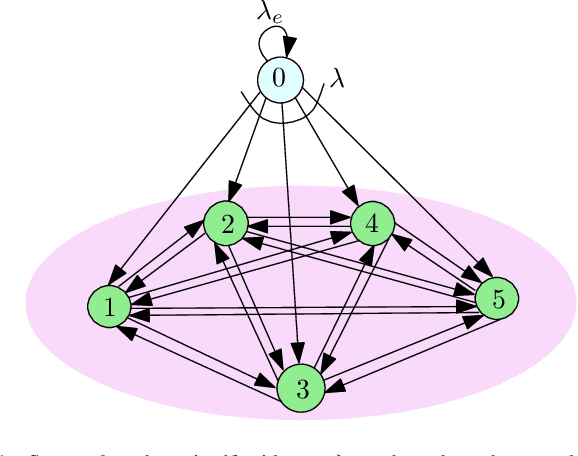
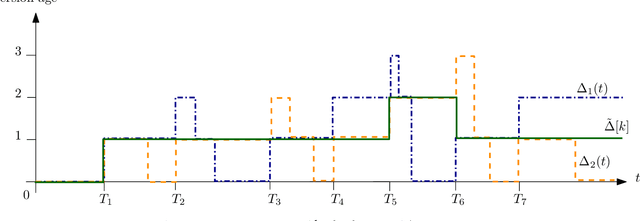
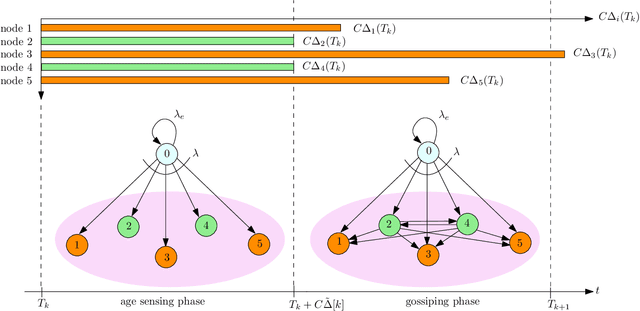
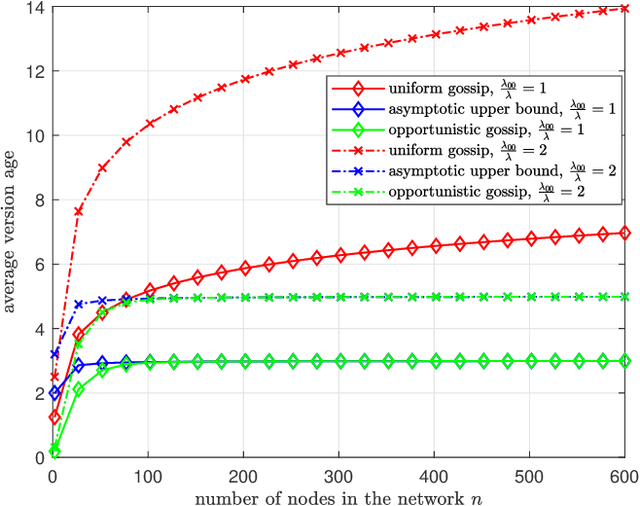
We consider a fully-connected wireless gossip network which consists of a source and $n$ receiver nodes. The source updates itself with a Poisson process and also sends updates to the nodes as Poisson arrivals. Upon receiving the updates, the nodes update their knowledge about the source. The nodes gossip the data among themselves in the form of Poisson arrivals to disperse their knowledge about the source. The total gossiping rate is bounded by a constraint. The goal of the network is to be as timely as possible with the source. In this work, we propose ASUMAN, a distributed opportunistic gossiping scheme, where after each time the source updates itself, each node waits for a time proportional to its current age and broadcasts a signal to the other nodes of the network. This allows the nodes in the network which have higher age to remain silent and only the low-age nodes to gossip, thus utilizing a significant portion of the constrained total gossip rate. We calculate the average age for a typical node in such a network with symmetric settings and show that the theoretical upper bound on the age scales as $O(1)$. ASUMAN, with an average age of $O(1)$, offers significant gains compared to a system where the nodes just gossip blindly with a fixed update rate in which case the age scales as $O(\log n)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge