InfoTok: Adaptive Discrete Video Tokenizer via Information-Theoretic Compression

Accurate and efficient discrete video tokenization is essential for long video sequences processing. Yet, the inherent complexity and variable information density of videos present a significant bottleneck for current tokenizers, which rigidly compress all content at a fixed rate, leading to redundancy or information loss. Drawing inspiration from Shannon's information theory, this paper introduces InfoTok, a principled framework for adaptive video tokenization. We rigorously prove that existing data-agnostic training methods are suboptimal in representation length, and present a novel evidence lower bound (ELBO)-based algorithm that approaches theoretical optimality. Leveraging this framework, we develop a transformer-based adaptive compressor that enables adaptive tokenization. Empirical results demonstrate state-of-the-art compression performance, saving 20% tokens without influence on performance, and achieving 2.3x compression rates while still outperforming prior heuristic adaptive approaches. By allocating tokens according to informational richness, InfoTok enables a more compressed yet accurate tokenization for video representation, offering valuable insights for future research.

Robust Sampling for Active Statistical Inference

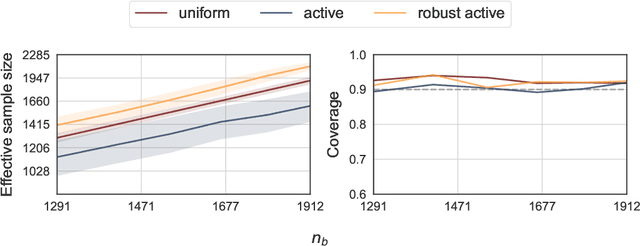
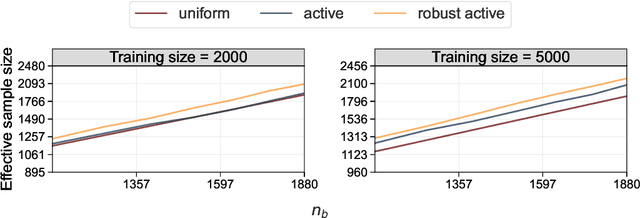
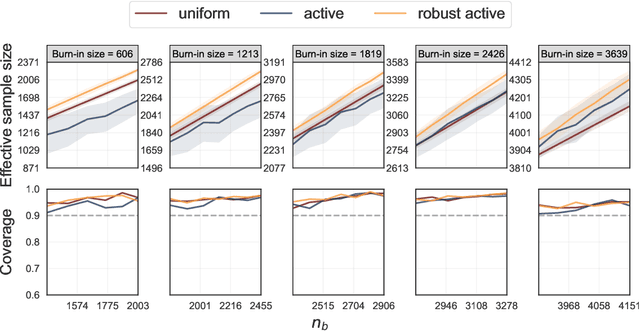
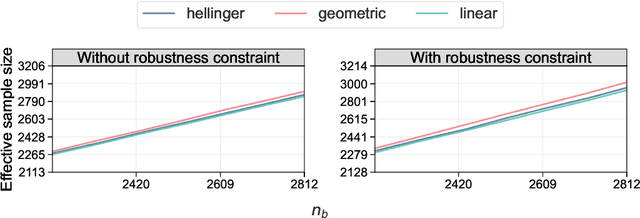
Active statistical inference is a new method for inference with AI-assisted data collection. Given a budget on the number of labeled data points that can be collected and assuming access to an AI predictive model, the basic idea is to improve estimation accuracy by prioritizing the collection of labels where the model is most uncertain. The drawback, however, is that inaccurate uncertainty estimates can make active sampling produce highly noisy results, potentially worse than those from naive uniform sampling. In this work, we present robust sampling strategies for active statistical inference. Robust sampling ensures that the resulting estimator is never worse than the estimator using uniform sampling. Furthermore, with reliable uncertainty estimates, the estimator usually outperforms standard active inference. This is achieved by optimally interpolating between uniform and active sampling, depending on the quality of the uncertainty scores, and by using ideas from robust optimization. We demonstrate the utility of the method on a series of real datasets from computational social science and survey research.

Analyzing the Role of Permutation Invariance in Linear Mode Connectivity

It was empirically observed in Entezari et al. (2021) that when accounting for the permutation invariance of neural networks, there is likely no loss barrier along the linear interpolation between two SGD solutions -- a phenomenon known as linear mode connectivity (LMC) modulo permutation. This phenomenon has sparked significant attention due to both its theoretical interest and practical relevance in applications such as model merging. In this paper, we provide a fine-grained analysis of this phenomenon for two-layer ReLU networks under a teacher-student setup. We show that as the student network width $m$ increases, the LMC loss barrier modulo permutation exhibits a {\bf double descent} behavior. Particularly, when $m$ is sufficiently large, the barrier decreases to zero at a rate $O(m^{-1/2})$. Notably, this rate does not suffer from the curse of dimensionality and demonstrates how substantial permutation can reduce the LMC loss barrier. Moreover, we observe a sharp transition in the sparsity of GD/SGD solutions when increasing the learning rate and investigate how this sparsity preference affects the LMC loss barrier modulo permutation. Experiments on both synthetic and MNIST datasets corroborate our theoretical predictions and reveal a similar trend for more complex network architectures.

Exploring Neural Network Landscapes: Star-Shaped and Geodesic Connectivity

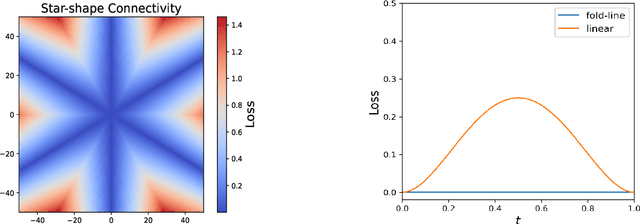
One of the most intriguing findings in the structure of neural network landscape is the phenomenon of mode connectivity: For two typical global minima, there exists a path connecting them without barrier. This concept of mode connectivity has played a crucial role in understanding important phenomena in deep learning. In this paper, we conduct a fine-grained analysis of this connectivity phenomenon. First, we demonstrate that in the overparameterized case, the connecting path can be as simple as a two-piece linear path, and the path length can be nearly equal to the Euclidean distance. This finding suggests that the landscape should be nearly convex in a certain sense. Second, we uncover a surprising star-shaped connectivity: For a finite number of typical minima, there exists a center on minima manifold that connects all of them simultaneously via linear paths. These results are provably valid for linear networks and two-layer ReLU networks under a teacher-student setup, and are empirically supported by models trained on MNIST and CIFAR-10.

On the Generalization Properties of Diffusion Models

Diffusion models are a class of generative models that serve to establish a stochastic transport map between an empirically observed, yet unknown, target distribution and a known prior. Despite their remarkable success in real-world applications, a theoretical understanding of their generalization capabilities remains underdeveloped. This work embarks on a comprehensive theoretical exploration of the generalization attributes of diffusion models. We establish theoretical estimates of the generalization gap that evolves in tandem with the training dynamics of score-based diffusion models, suggesting a polynomially small generalization error ($O(n^{-2/5}+m^{-4/5})$) on both the sample size $n$ and the model capacity $m$, evading the curse of dimensionality (i.e., not exponentially large in the data dimension) when early-stopped. Furthermore, we extend our quantitative analysis to a data-dependent scenario, wherein target distributions are portrayed as a succession of densities with progressively increasing distances between modes. This precisely elucidates the adverse effect of "modes shift" in ground truths on the model generalization. Moreover, these estimates are not solely theoretical constructs but have also been confirmed through numerical simulations. Our findings contribute to the rigorous understanding of diffusion models' generalization properties and provide insights that may guide practical applications.

FaiREE: Fair Classification with Finite-Sample and Distribution-Free Guarantee

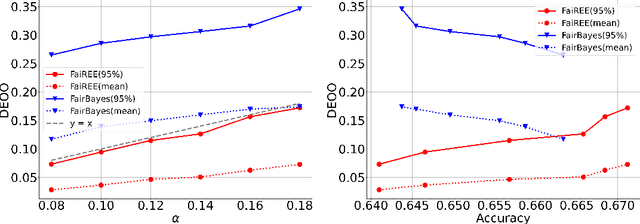
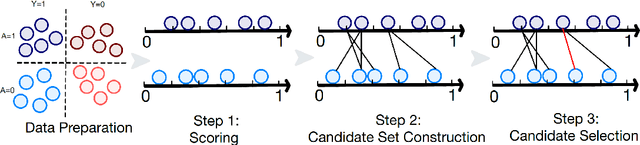
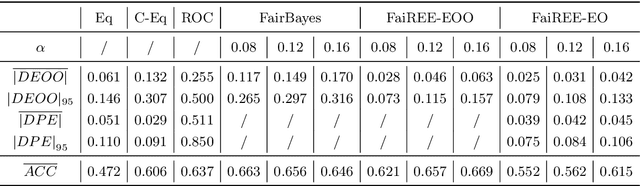
Algorithmic fairness plays an increasingly critical role in machine learning research. Several group fairness notions and algorithms have been proposed. However, the fairness guarantee of existing fair classification methods mainly depends on specific data distributional assumptions, often requiring large sample sizes, and fairness could be violated when there is a modest number of samples, which is often the case in practice. In this paper, we propose FaiREE, a fair classification algorithm that can satisfy group fairness constraints with finite-sample and distribution-free theoretical guarantees. FaiREE can be adapted to satisfy various group fairness notions (e.g., Equality of Opportunity, Equalized Odds, Demographic Parity, etc.) and achieve the optimal accuracy. These theoretical guarantees are further supported by experiments on both synthetic and real data. FaiREE is shown to have favorable performance over state-of-the-art algorithms.