On the Stability of the Jacobian Matrix in Deep Neural Networks

Deep neural networks are known to suffer from exploding or vanishing gradients as depth increases, a phenomenon closely tied to the spectral behavior of the input-output Jacobian. Prior work has identified critical initialization schemes that ensure Jacobian stability, but these analyses are typically restricted to fully connected networks with i.i.d. weights. In this work, we go significantly beyond these limitations: we establish a general stability theorem for deep neural networks that accommodates sparsity (such as that introduced by pruning) and non-i.i.d., weakly correlated weights (e.g. induced by training). Our results rely on recent advances in random matrix theory, and provide rigorous guarantees for spectral stability in a much broader class of network models. This extends the theoretical foundation for initialization schemes in modern neural networks with structured and dependent randomness.

Finite-Sample Analysis of the Monte Carlo Exploring Starts Algorithm for Reinforcement Learning

Monte Carlo Exploring Starts (MCES), which aims to learn the optimal policy using only sample returns, is a simple and natural algorithm in reinforcement learning which has been shown to converge under various conditions. However, the convergence rate analysis for MCES-style algorithms in the form of sample complexity has received very little attention. In this paper we develop a finite sample bound for a modified MCES algorithm which solves the stochastic shortest path problem. To this end, we prove a novel result on the convergence rate of the policy iteration algorithm. This result implies that with probability at least $1-\delta$, the algorithm returns an optimal policy after $\tilde{O}(SAK^3\log^3\frac{1}{\delta})$ sampled episodes, where $S$ and $A$ denote the number of states and actions respectively, $K$ is a proxy for episode length, and $\tilde{O}$ hides logarithmic factors and constants depending on the rewards of the environment that are assumed to be known.

How Bad is Training on Synthetic Data? A Statistical Analysis of Language Model Collapse

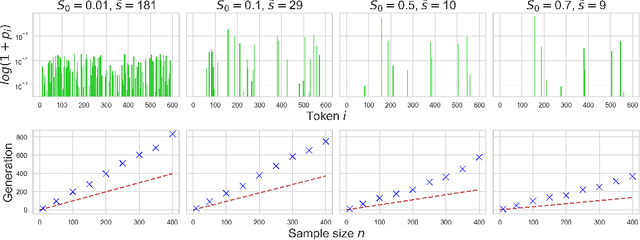
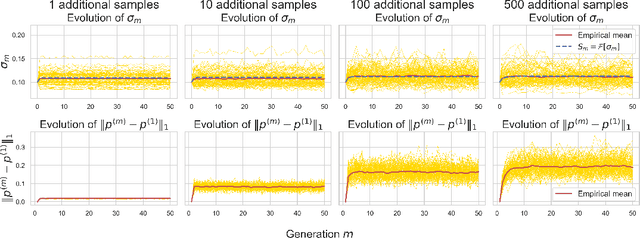
The phenomenon of model collapse, introduced in (Shumailov et al., 2023), refers to the deterioration in performance that occurs when new models are trained on synthetic data generated from previously trained models. This recursive training loop makes the tails of the original distribution disappear, thereby making future-generation models forget about the initial (real) distribution. With the aim of rigorously understanding model collapse in language models, we consider in this paper a statistical model that allows us to characterize the impact of various recursive training scenarios. Specifically, we demonstrate that model collapse cannot be avoided when training solely on synthetic data. However, when mixing both real and synthetic data, we provide an estimate of a maximal amount of synthetic data below which model collapse can eventually be avoided. Our theoretical conclusions are further supported by empirical validations.