Evaluation of Deep Neural Operator Models toward Ocean Forecasting

Data-driven, deep-learning modeling frameworks have been recently developed for forecasting time series data. Such machine learning models may be useful in multiple domains including the atmospheric and oceanic ones, and in general, the larger fluids community. The present work investigates the possible effectiveness of such deep neural operator models for reproducing and predicting classic fluid flows and simulations of realistic ocean dynamics. We first briefly evaluate the capabilities of such deep neural operator models when trained on a simulated two-dimensional fluid flow past a cylinder. We then investigate their application to forecasting ocean surface circulation in the Middle Atlantic Bight and Massachusetts Bay, learning from high-resolution data-assimilative simulations employed for real sea experiments. We confirm that trained deep neural operator models are capable of predicting idealized periodic eddy shedding. For realistic ocean surface flows and our preliminary study, they can predict several of the features and show some skill, providing potential for future research and applications.

Maximizing Seaweed Growth on Autonomous Farms: A Dynamic Programming Approach for Underactuated Systems Navigating on Uncertain Ocean Currents

Seaweed biomass offers significant potential for climate mitigation, but large-scale, autonomous open-ocean farms are required to fully exploit it. Such farms typically have low propulsion and are heavily influenced by ocean currents. We want to design a controller that maximizes seaweed growth over months by taking advantage of the non-linear time-varying ocean currents for reaching high-growth regions. The complex dynamics and underactuation make this challenging even when the currents are known. This is even harder when only short-term imperfect forecasts with increasing uncertainty are available. We propose a dynamic programming-based method to efficiently solve for the optimal growth value function when true currents are known. We additionally present three extensions when as in reality only forecasts are known: (1) our methods resulting value function can be used as feedback policy to obtain the growth-optimal control for all states and times, allowing closed-loop control equivalent to re-planning at every time step hence mitigating forecast errors, (2) a feedback policy for long-term optimal growth beyond forecast horizons using seasonal average current data as terminal reward, and (3) a discounted finite-time Dynamic Programming (DP) formulation to account for increasing ocean current estimate uncertainty. We evaluate our approach through 30-day simulations of floating seaweed farms in realistic Pacific Ocean current scenarios. Our method demonstrates an achievement of 95.8% of the best possible growth using only 5-day forecasts. This confirms the feasibility of using low-power propulsion and optimal control for enhanced seaweed growth on floating farms under real-world conditions.

Stranding Risk for Underactuated Vessels in Complex Ocean Currents: Analysis and Controllers

Low-propulsion vessels can take advantage of powerful ocean currents to navigate towards a destination. Recent results demonstrated that vessels can reach their destination with high probability despite forecast errors. However, these results do not consider the critical aspect of safety of such vessels: because of their low propulsion which is much smaller than the magnitude of currents, they might end up in currents that inevitably push them into unsafe areas such as shallow areas, garbage patches, and shipping lanes. In this work, we first investigate the risk of stranding for free-floating vessels in the Northeast Pacific. We find that at least 5.04% would strand within 90 days. Next, we encode the unsafe sets as hard constraints into Hamilton-Jacobi Multi-Time Reachability (HJ-MTR) to synthesize a feedback policy that is equivalent to re-planning at each time step at low computational cost. While applying this policy closed-loop guarantees safe operation when the currents are known, in realistic situations only imperfect forecasts are available. We demonstrate the safety of our approach in such realistic situations empirically with large-scale simulations of a vessel navigating in high-risk regions in the Northeast Pacific. We find that applying our policy closed-loop with daily re-planning on new forecasts can ensure safety with high probability even under forecast errors that exceed the maximal propulsion. Our method significantly improves safety over the baselines and still achieves a timely arrival of the vessel at the destination.

Generalized Neural Closure Models with Interpretability

Improving the predictive capability and computational cost of dynamical models is often at the heart of augmenting computational physics with machine learning (ML). However, most learning results are limited in interpretability and generalization over different computational grid resolutions, initial and boundary conditions, domain geometries, and physical or problem-specific parameters. In the present study, we simultaneously address all these challenges by developing the novel and versatile methodology of unified neural partial delay differential equations. We augment existing/low-fidelity dynamical models directly in their partial differential equation (PDE) forms with both Markovian and non-Markovian neural network (NN) closure parameterizations. The melding of the existing models with NNs in the continuous spatiotemporal space followed by numerical discretization automatically allows for the desired generalizability. The Markovian term is designed to enable extraction of its analytical form and thus provides interpretability. The non-Markovian terms allow accounting for inherently missing time delays needed to represent the real world. We obtain adjoint PDEs in the continuous form, thus enabling direct implementation across differentiable and non-differentiable computational physics codes, different ML frameworks, and treatment of nonuniformly-spaced spatiotemporal training data. We demonstrate the new generalized neural closure models (gnCMs) framework using four sets of experiments based on advecting nonlinear waves, shocks, and ocean acidification models. Our learned gnCMs discover missing physics, find leading numerical error terms, discriminate among candidate functional forms in an interpretable fashion, achieve generalization, and compensate for the lack of complexity in simpler models. Finally, we analyze the computational advantages of our new framework.

Bayesian Learning of Coupled Biogeochemical-Physical Models

Predictive models for marine ecosystems are used for a variety of needs. Due to sparse measurements and limited understanding of the myriad of ocean processes, there is however uncertainty. There is model uncertainty in the parameter values, functional forms with diverse parameterizations, level of complexity needed, and thus in the state fields. We develop a principled Bayesian model learning methodology that allows interpolation in the space of candidate models and discovery of new models, all while estimating state fields and parameter values, as well as the joint probability distributions of all learned quantities. We address the challenges of high-dimensional and multidisciplinary dynamics governed by partial differential equations (PDEs) by using state augmentation and the computationally efficient Gaussian Mixture Model - Dynamically Orthogonal filter. Our innovations include special stochastic parameters to unify candidate models into a single general model and stochastic piecewise function approximations to generate dense candidate model spaces. They allow handling many candidate models, possibly none of which are accurate, and learning elusive unknown functional forms in compatible and embedded models. Our new methodology is generalizable and interpretable and extrapolates out of the space of models to discover new ones. We perform a series of twin experiments based on flows past a seamount coupled with three-to-five component ecosystem models, including flows with chaotic advection. We quantify learning skills, and evaluate convergence and sensitivity to hyper-parameters. Our PDE framework successfully discriminates among model candidates, learns in the absence of prior knowledge by searching in dense function spaces, and updates joint probabilities while capturing non-Gaussian statistics. The parameter values and model formulations that best explain the data are identified.

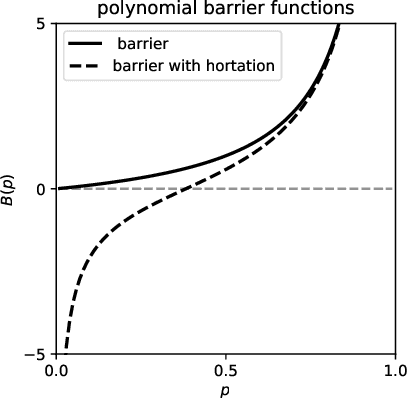
Deep Reinforcement Learning for Adaptive Mesh Refinement

Finite element discretizations of problems in computational physics often rely on adaptive mesh refinement (AMR) to preferentially resolve regions containing important features during simulation. However, these spatial refinement strategies are often heuristic and rely on domain-specific knowledge or trial-and-error. We treat the process of adaptive mesh refinement as a local, sequential decision-making problem under incomplete information, formulating AMR as a partially observable Markov decision process. Using a deep reinforcement learning approach, we train policy networks for AMR strategy directly from numerical simulation. The training process does not require an exact solution or a high-fidelity ground truth to the partial differential equation at hand, nor does it require a pre-computed training dataset. The local nature of our reinforcement learning formulation allows the policy network to be trained inexpensively on much smaller problems than those on which they are deployed. The methodology is not specific to any particular partial differential equation, problem dimension, or numerical discretization, and can flexibly incorporate diverse problem physics. To that end, we apply the approach to a diverse set of partial differential equations, using a variety of high-order discontinuous Galerkin and hybridizable discontinuous Galerkin finite element discretizations. We show that the resultant deep reinforcement learning policies are competitive with common AMR heuristics, generalize well across problem classes, and strike a favorable balance between accuracy and cost such that they often lead to a higher accuracy per problem degree of freedom.

Neural Closure Models for Dynamical Systems

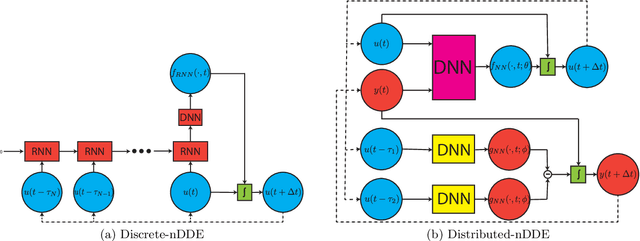
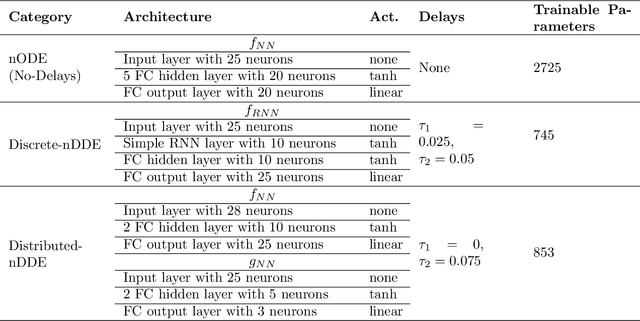
Complex dynamical systems are used for predictions in many applications. Because of computational costs, models are however often truncated, coarsened, or aggregated. As the neglected and unresolved terms along with their interactions with the resolved ones become important, the usefulness of model predictions diminishes. We develop a novel, versatile, and rigorous methodology to learn non-Markovian closure parameterizations for low-fidelity models using data from high-fidelity simulations. The new "neural closure models" augment low-fidelity models with neural delay differential equations (nDDEs), motivated by the Mori-Zwanzig formulation and the inherent delays in natural dynamical systems. We demonstrate that neural closures efficiently account for truncated modes in reduced-order-models, capture the effects of subgrid-scale processes in coarse models, and augment the simplification of complex biochemical models. We show that using non-Markovian over Markovian closures improves long-term accuracy and requires smaller networks. We provide adjoint equation derivations and network architectures needed to efficiently implement the new discrete and distributed nDDEs. The performance of discrete over distributed delays in closure models is explained using information theory, and we observe an optimal amount of past information for a specified architecture. Finally, we analyze computational complexity and explain the limited additional cost due to neural closure models.