Neural Closure Models for Dynamical Systems

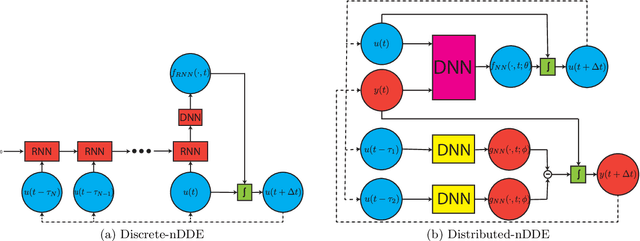
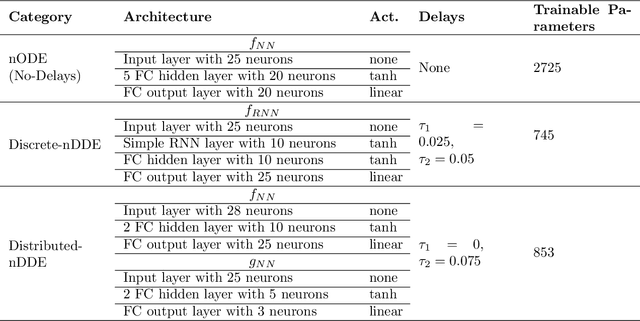
Complex dynamical systems are used for predictions in many applications. Because of computational costs, models are however often truncated, coarsened, or aggregated. As the neglected and unresolved terms along with their interactions with the resolved ones become important, the usefulness of model predictions diminishes. We develop a novel, versatile, and rigorous methodology to learn non-Markovian closure parameterizations for low-fidelity models using data from high-fidelity simulations. The new "neural closure models" augment low-fidelity models with neural delay differential equations (nDDEs), motivated by the Mori-Zwanzig formulation and the inherent delays in natural dynamical systems. We demonstrate that neural closures efficiently account for truncated modes in reduced-order-models, capture the effects of subgrid-scale processes in coarse models, and augment the simplification of complex biochemical models. We show that using non-Markovian over Markovian closures improves long-term accuracy and requires smaller networks. We provide adjoint equation derivations and network architectures needed to efficiently implement the new discrete and distributed nDDEs. The performance of discrete over distributed delays in closure models is explained using information theory, and we observe an optimal amount of past information for a specified architecture. Finally, we analyze computational complexity and explain the limited additional cost due to neural closure models.