Towards Faster Matrix Diagonalization with Graph Isomorphism Networks and the AlphaZero Framework

In this paper, we introduce innovative approaches for accelerating the Jacobi method for matrix diagonalization, specifically through the formulation of large matrix diagonalization as a Semi-Markov Decision Process and small matrix diagonalization as a Markov Decision Process. Furthermore, we examine the potential of utilizing scalable architecture between different-sized matrices. During a short training period, our method discovered a significant reduction in the number of steps required for diagonalization and exhibited efficient inference capabilities. Importantly, this approach demonstrated possible scalability to large-sized matrices, indicating its potential for wide-ranging applicability. Upon training completion, we obtain action-state probabilities and transition graphs, which depict transitions between different states. These outputs not only provide insights into the diagonalization process but also pave the way for cost savings pertinent to large-scale matrices. The advancements made in this research enhance the efficacy and scalability of matrix diagonalization, pushing for new possibilities for deployment in practical applications in scientific and engineering domains.

Accelerating Matrix Diagonalization through Decision Transformers with Epsilon-Greedy Optimization

This paper introduces a novel framework for matrix diagonalization, recasting it as a sequential decision-making problem and applying the power of Decision Transformers (DTs). Our approach determines optimal pivot selection during diagonalization with the Jacobi algorithm, leading to significant speedups compared to the traditional max-element Jacobi method. To bolster robustness, we integrate an epsilon-greedy strategy, enabling success in scenarios where deterministic approaches fail. This work demonstrates the effectiveness of DTs in complex computational tasks and highlights the potential of reimagining mathematical operations through a machine learning lens. Furthermore, we establish the generalizability of our method by using transfer learning to diagonalize matrices of smaller sizes than those trained.

Matrix Diagonalization as a Board Game: Teaching an Eigensolver the Fastest Path to Solution

Matrix diagonalization is at the cornerstone of numerous fields of scientific computing. Diagonalizing a matrix to solve an eigenvalue problem requires a sequential path of iterations that eventually reaches a sufficiently converged and accurate solution for all the eigenvalues and eigenvectors. This typically translates into a high computational cost. Here we demonstrate how reinforcement learning, using the AlphaZero framework, can accelerate Jacobi matrix diagonalizations by viewing the selection of the fastest path to solution as a board game. To demonstrate the viability of our approach we apply the Jacobi diagonalization algorithm to symmetric Hamiltonian matrices that appear in quantum chemistry calculations. We find that a significant acceleration can often be achieved. Our findings highlight the opportunity to use machine learning as a promising tool to improve the performance of numerical linear algebra.

The ISTI Rapid Response on Exploring Cloud Computing 2018

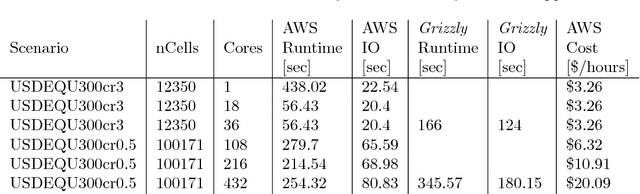
This report describes eighteen projects that explored how commercial cloud computing services can be utilized for scientific computation at national laboratories. These demonstrations ranged from deploying proprietary software in a cloud environment to leveraging established cloud-based analytics workflows for processing scientific datasets. By and large, the projects were successful and collectively they suggest that cloud computing can be a valuable computational resource for scientific computation at national laboratories.