SPAD: Seven-Source Token Probability Attribution with Syntactic Aggregation for Detecting Hallucinations in RAG

Detecting hallucinations in Retrieval-Augmented Generation (RAG) remains a challenge. Prior approaches attribute hallucinations to a binary conflict between internal knowledge (stored in FFNs) and retrieved context. However, this perspective is incomplete, failing to account for the impact of other components in the generative process, such as the user query, previously generated tokens, the current token itself, and the final LayerNorm adjustment. To address this, we introduce SPAD. First, we mathematically attribute each token's probability into seven distinct sources: Query, RAG, Past, Current Token, FFN, Final LayerNorm, and Initial Embedding. This attribution quantifies how each source contributes to the generation of the current token. Then, we aggregate these scores by POS tags to quantify how different components drive specific linguistic categories. By identifying anomalies, such as Nouns relying on Final LayerNorm, SPAD effectively detects hallucinations. Extensive experiments demonstrate that SPAD achieves state-of-the-art performance

Autonomous Concept Drift Threshold Determination

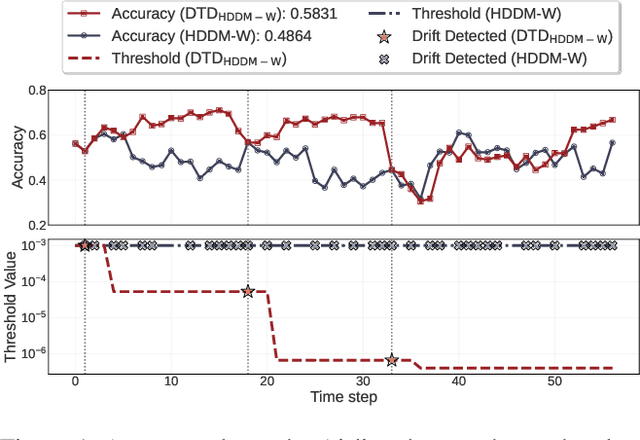
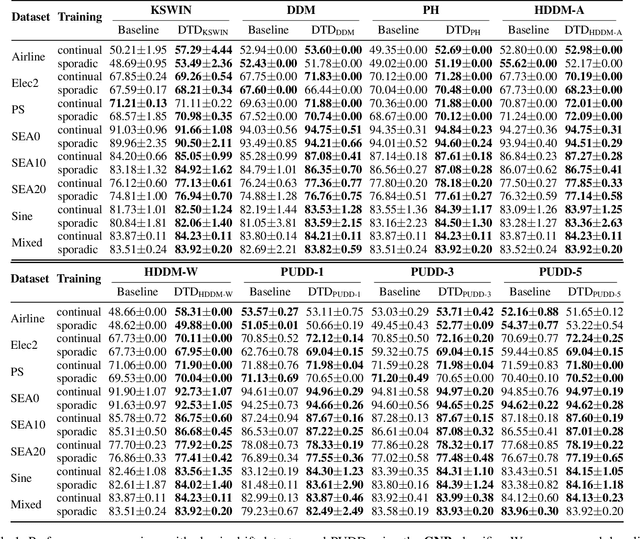
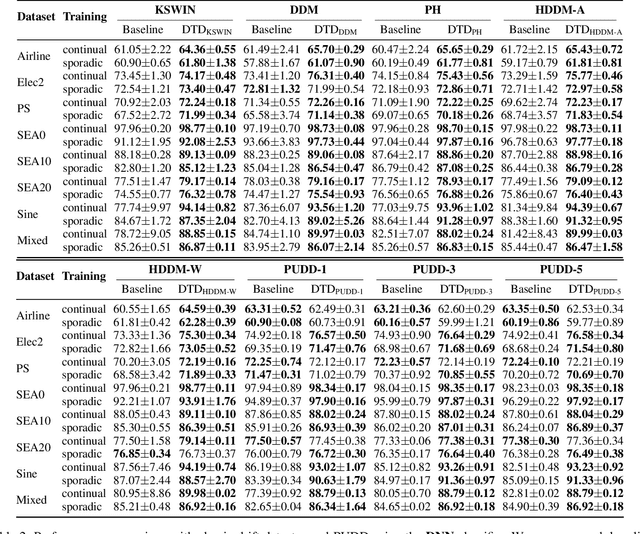
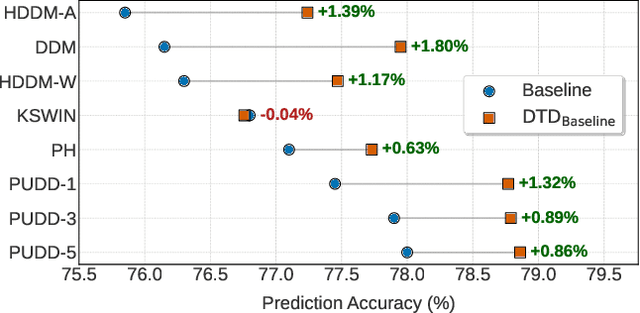
Existing drift detection methods focus on designing sensitive test statistics. They treat the detection threshold as a fixed hyperparameter, set once to balance false alarms and late detections, and applied uniformly across all datasets and over time. However, maintaining model performance is the key objective from the perspective of machine learning, and we observe that model performance is highly sensitive to this threshold. This observation inspires us to investigate whether a dynamic threshold could be provably better. In this paper, we prove that a threshold that adapts over time can outperform any single fixed threshold. The main idea of the proof is that a dynamic strategy, constructed by combining the best threshold from each individual data segment, is guaranteed to outperform any single threshold that apply to all segments. Based on the theorem, we propose a Dynamic Threshold Determination algorithm. It enhances existing drift detection frameworks with a novel comparison phase to inform how the threshold should be adjusted. Extensive experiments on a wide range of synthetic and real-world datasets, including both image and tabular data, validate that our approach substantially enhances the performance of state-of-the-art drift detectors.

Early Concept Drift Detection via Prediction Uncertainty

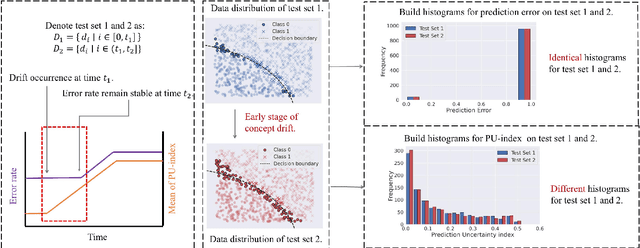
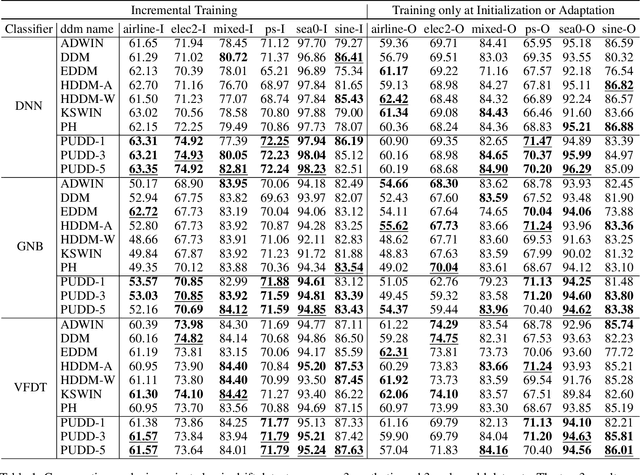
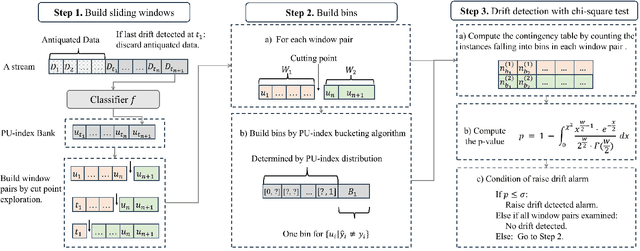
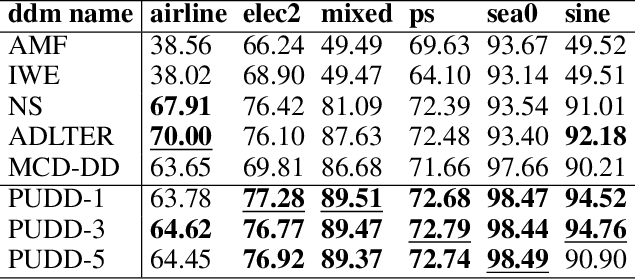
Concept drift, characterized by unpredictable changes in data distribution over time, poses significant challenges to machine learning models in streaming data scenarios. Although error rate-based concept drift detectors are widely used, they often fail to identify drift in the early stages when the data distribution changes but error rates remain constant. This paper introduces the Prediction Uncertainty Index (PU-index), derived from the prediction uncertainty of the classifier, as a superior alternative to the error rate for drift detection. Our theoretical analysis demonstrates that: (1) The PU-index can detect drift even when error rates remain stable. (2) Any change in the error rate will lead to a corresponding change in the PU-index. These properties make the PU-index a more sensitive and robust indicator for drift detection compared to existing methods. We also propose a PU-index-based Drift Detector (PUDD) that employs a novel Adaptive PU-index Bucketing algorithm for detecting drift. Empirical evaluations on both synthetic and real-world datasets demonstrate PUDD's efficacy in detecting drift in structured and image data.

Regularly Truncated M-estimators for Learning with Noisy Labels

The sample selection approach is very popular in learning with noisy labels. As deep networks learn pattern first, prior methods built on sample selection share a similar training procedure: the small-loss examples can be regarded as clean examples and used for helping generalization, while the large-loss examples are treated as mislabeled ones and excluded from network parameter updates. However, such a procedure is arguably debatable from two folds: (a) it does not consider the bad influence of noisy labels in selected small-loss examples; (b) it does not make good use of the discarded large-loss examples, which may be clean or have meaningful information for generalization. In this paper, we propose regularly truncated M-estimators (RTME) to address the above two issues simultaneously. Specifically, RTME can alternately switch modes between truncated M-estimators and original M-estimators. The former can adaptively select small-losses examples without knowing the noise rate and reduce the side-effects of noisy labels in them. The latter makes the possibly clean examples but with large losses involved to help generalization. Theoretically, we demonstrate that our strategies are label-noise-tolerant. Empirically, comprehensive experimental results show that our method can outperform multiple baselines and is robust to broad noise types and levels.