DG-STMTL: A Novel Graph Convolutional Network for Multi-Task Spatio-Temporal Traffic Forecasting

Spatio-temporal traffic prediction is crucial in intelligent transportation systems. The key challenge of accurate prediction is how to model the complex spatio-temporal dependencies and adapt to the inherent dynamics in data. Traditional Graph Convolutional Networks (GCNs) often struggle with static adjacency matrices that introduce domain bias or learnable matrices that may be overfitting to specific patterns. This challenge becomes more complex when considering Multi-Task Learning (MTL). While MTL has the potential to enhance prediction accuracy through task synergies, it can also face significant hurdles due to task interference. To overcome these challenges, this study introduces a novel MTL framework, Dynamic Group-wise Spatio-Temporal Multi-Task Learning (DG-STMTL). DG-STMTL proposes a hybrid adjacency matrix generation module that combines static matrices with dynamic ones through a task-specific gating mechanism. We also introduce a group-wise GCN module to enhance the modelling capability of spatio-temporal dependencies. We conduct extensive experiments on two real-world datasets to evaluate our method. Results show that our method outperforms other state-of-the-arts, indicating its effectiveness and robustness.

Constructing Data Transaction Chains Based on Opportunity Cost Exploration

Data trading is increasingly gaining attention. However, the inherent replicability and privacy concerns of data make it challenging to directly apply traditional trading theories to data markets. This paper compares data trading markets with traditional ones, focusing particularly on how the replicability and privacy of data impact data markets. We discuss how data's replicability fundamentally alters the concept of opportunity cost in traditional microeconomics within the context of data markets. Additionally, we explore how to leverage this change to maximize benefits without compromising data privacy. This paper outlines the constraints for data circulation within the privacy domain chain and presents a model that maximizes data's value under these constraints. Specific application scenarios are provided, and experiments demonstrate the solvability of this model.

Towards Efficient Deep Hashing Retrieval: Condensing Your Data via Feature-Embedding Matching

The expenses involved in training state-of-the-art deep hashing retrieval models have witnessed an increase due to the adoption of more sophisticated models and large-scale datasets. Dataset Distillation (DD) or Dataset Condensation(DC) focuses on generating smaller synthetic dataset that retains the original information. Nevertheless, existing DD methods face challenges in maintaining a trade-off between accuracy and efficiency. And the state-of-the-art dataset distillation methods can not expand to all deep hashing retrieval methods. In this paper, we propose an efficient condensation framework that addresses these limitations by matching the feature-embedding between synthetic set and real set. Furthermore, we enhance the diversity of features by incorporating the strategies of early-stage augmented models and multi-formation. Extensive experiments provide compelling evidence of the remarkable superiority of our approach, both in terms of performance and efficiency, compared to state-of-the-art baseline methods.

Data valuation: The partial ordinal Shapley value for machine learning

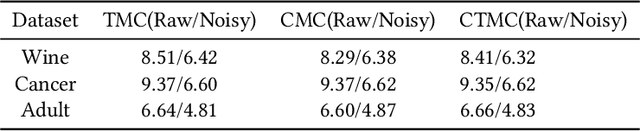
Data valuation using Shapley value has emerged as a prevalent research domain in machine learning applications. However, it is a challenge to address the role of order in data cooperation as most research lacks such discussion. To tackle this problem, this paper studies the definition of the partial ordinal Shapley value by group theory in abstract algebra. Besides, since the calculation of the partial ordinal Shapley value requires exponential time, this paper also gives three algorithms for approximating the results. The Truncated Monte Carlo algorithm is derived from the classic Shapley value approximation algorithm. The Classification Monte Carlo algorithm and the Classification Truncated Monte Carlo algorithm are based on the fact that the data points in the same class provide similar information, then we can accelerate the calculation by leaving out some data points in each class.