ClusterGraph: a new tool for visualization and compression of multidimensional data

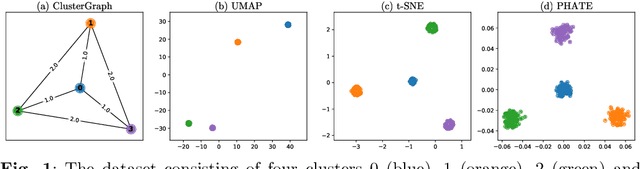
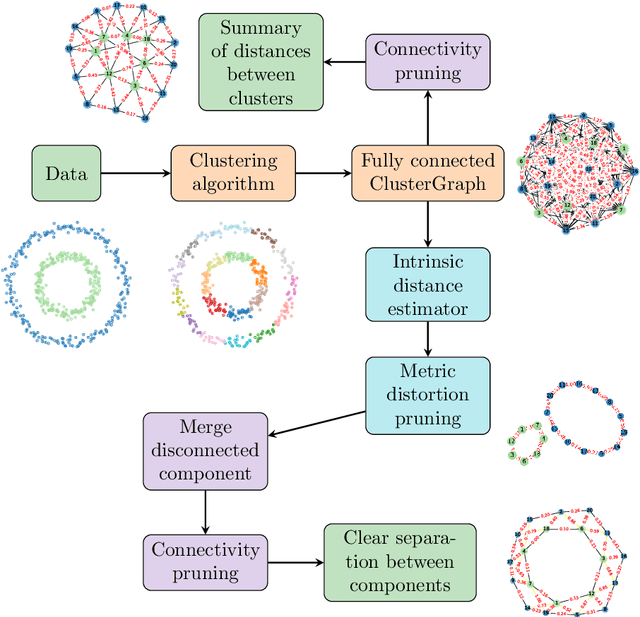
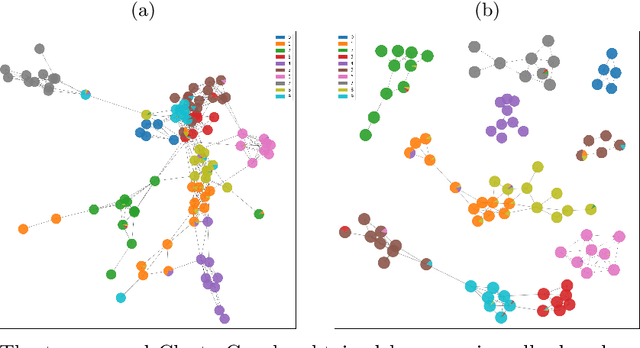
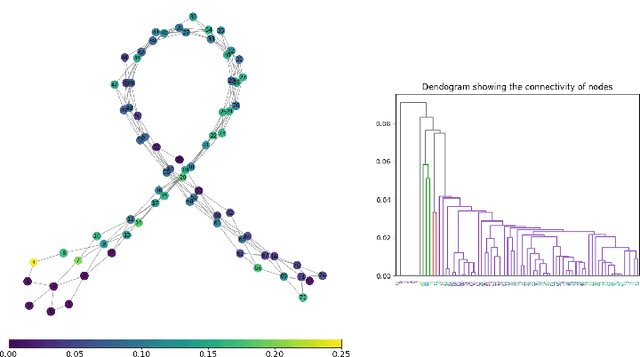
Understanding the global organization of complicated and high dimensional data is of primary interest for many branches of applied sciences. It is typically achieved by applying dimensionality reduction techniques mapping the considered data into lower dimensional space. This family of methods, while preserving local structures and features, often misses the global structure of the dataset. Clustering techniques are another class of methods operating on the data in the ambient space. They group together points that are similar according to a fixed similarity criteria, however unlike dimensionality reduction techniques, they do not provide information about the global organization of the data. Leveraging ideas from Topological Data Analysis, in this paper we provide an additional layer on the output of any clustering algorithm. Such data structure, ClusterGraph, provides information about the global layout of clusters, obtained from the considered clustering algorithm. Appropriate measures are provided to assess the quality and usefulness of the obtained representation. Subsequently the ClusterGraph, possibly with an appropriate structure--preserving simplification, can be visualized and used in synergy with state of the art exploratory data analysis techniques.

Euler Characteristic Curves and Profiles: a stable shape invariant for big data problems

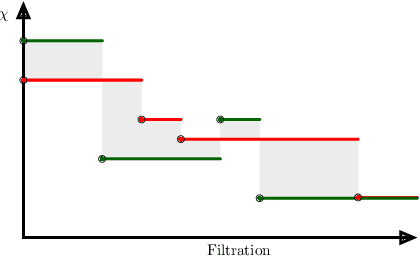
Tools of Topological Data Analysis provide stable summaries encapsulating the shape of the considered data. Persistent homology, the most standard and well studied data summary, suffers a number of limitations; its computations are hard to distribute, it is hard to generalize to multifiltrations and is computationally prohibitive for big data-sets. In this paper we study the concept of Euler Characteristics Curves, for one parameter filtrations and Euler Characteristic Profiles, for multi-parameter filtrations. While being a weaker invariant in one dimension, we show that Euler Characteristic based approaches do not possess some handicaps of persistent homology; we show efficient algorithms to compute them in a distributed way, their generalization to multifiltrations and practical applicability for big data problems. In addition we show that the Euler Curves and Profiles enjoys certain type of stability which makes them robust tool in data analysis. Lastly, to show their practical applicability, multiple use-cases are considered.

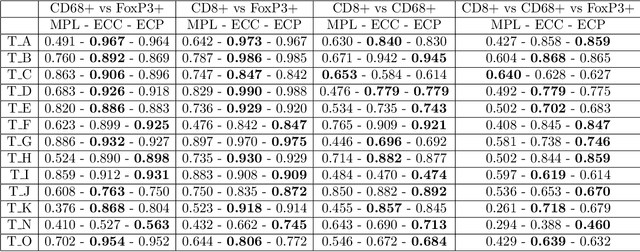
Hotspot identification for Mapper graphs

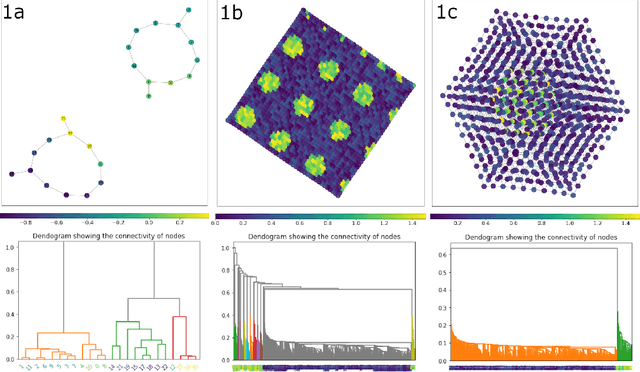
Mapper algorithm can be used to build graph-based representations of high-dimensional data capturing structurally interesting features such as loops, flares or clusters. The graph can be further annotated with additional colouring of vertices allowing location of regions of special interest. For instance, in many applications, such as precision medicine, Mapper graph has been used to identify unknown compactly localized subareas within the dataset demonstrating unique or unusual behaviours. This task, performed so far by a researcher, can be automatized using hotspot analysis. In this work we propose a new algorithm for detecting hotspots in Mapper graphs. It allows automatizing of the hotspot detection process. We demonstrate the performance of the algorithm on a number of artificial and real world datasets. We further demonstrate how our algorithm can be used for the automatic selection of the Mapper lens functions.

Persistence Bag-of-Words for Topological Data Analysis

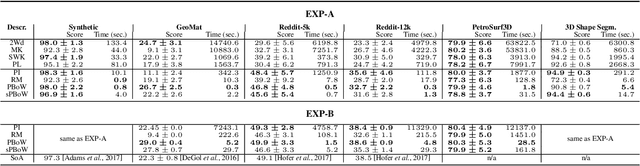
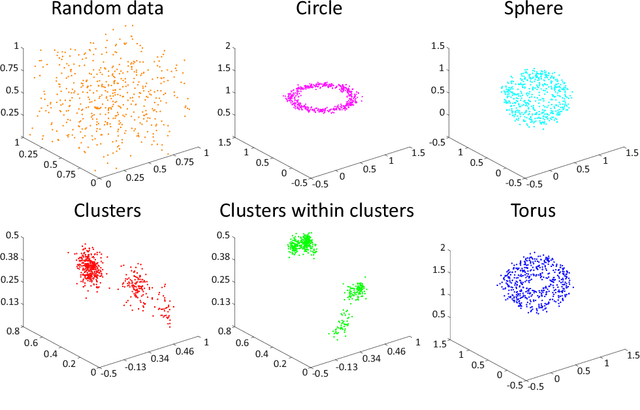
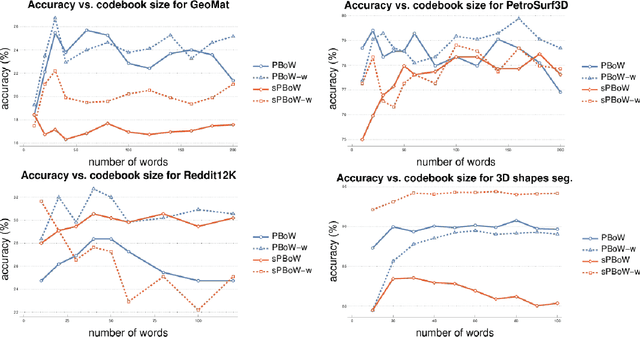
Persistent homology (PH) is a rigorous mathematical theory that provides a robust descriptor of data in the form of persistence diagrams (PDs). PDs are compact 2D representations formed by multisets of points. Their variable size makes them, however, difficult to combine with typical machine learning workflows. In this paper, we introduce persistence bag-of-words, which is a novel, expressive and discriminative vectorized representation of PDs for topological data analysis. It represents PDs in a convenient way for machine learning and statistical analysis and has a number of favorable practical and theoretical properties like 1-Wasserstein stability. We evaluate our representation on several heterogeneous datasets and show its high discriminative power. Our approach achieves state-of-the-art performance and even beyond in much less time than alternative approaches. Thereby, it facilitates the topological analysis of large-scale data sets in future.

Topology preserving thinning for cell complexes

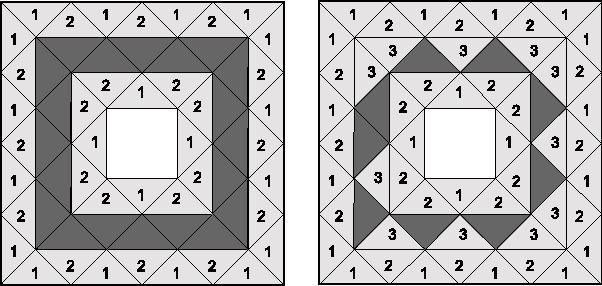
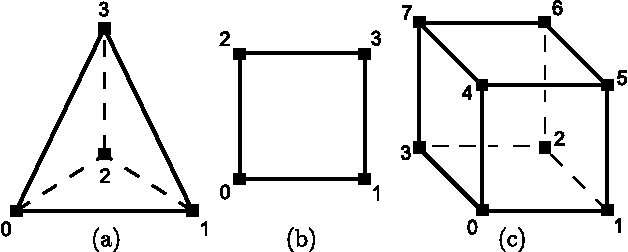
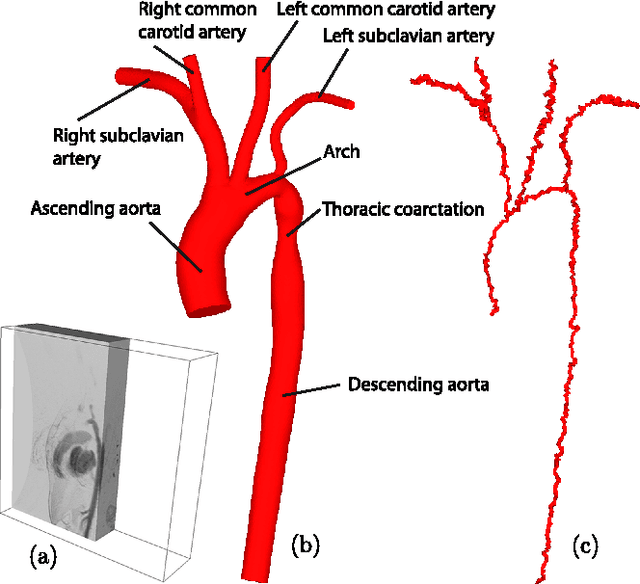
A topology preserving skeleton is a synthetic representation of an object that retains its topology and many of its significant morphological properties. The process of obtaining the skeleton, referred to as skeletonization or thinning, is a very active research area. It plays a central role in reducing the amount of information to be processed during image analysis and visualization, computer-aided diagnosis or by pattern recognition algorithms. This paper introduces a novel topology preserving thinning algorithm which removes \textit{simple cells}---a generalization of simple points---of a given cell complex. The test for simple cells is based on \textit{acyclicity tables} automatically produced in advance with homology computations. Using acyclicity tables render the implementation of thinning algorithms straightforward. Moreover, the fact that tables are automatically filled for all possible configurations allows to rigorously prove the generality of the algorithm and to obtain fool-proof implementations. The novel approach enables, for the first time, according to our knowledge, to thin a general unstructured simplicial complex. Acyclicity tables for cubical and simplicial complexes and an open source implementation of the thinning algorithm are provided as additional material to allow their immediate use in the vast number of practical applications arising in medical imaging and beyond.