Unsupervised Features Learning for Sampled Vector Fields

In this paper we introduce a new approach to computing hidden features of sampled vector fields. The basic idea is to convert the vector field data to a graph structure and use tools designed for automatic, unsupervised analysis of graphs. Using a few data sets we show that the collected features of the vector fields are correlated with the dynamics known for analytic models which generates the data. In particular the method may be useful in analysis of data sets where the analytic model is poorly understood or not known.

Persistence Bag-of-Words for Topological Data Analysis

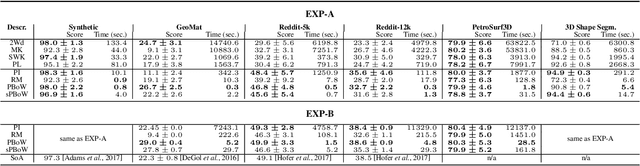
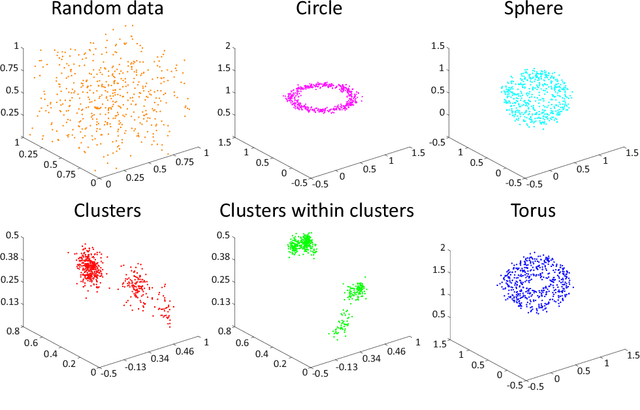
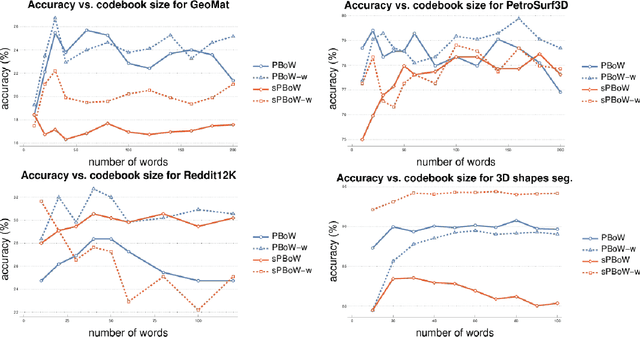
Persistent homology (PH) is a rigorous mathematical theory that provides a robust descriptor of data in the form of persistence diagrams (PDs). PDs are compact 2D representations formed by multisets of points. Their variable size makes them, however, difficult to combine with typical machine learning workflows. In this paper, we introduce persistence bag-of-words, which is a novel, expressive and discriminative vectorized representation of PDs for topological data analysis. It represents PDs in a convenient way for machine learning and statistical analysis and has a number of favorable practical and theoretical properties like 1-Wasserstein stability. We evaluate our representation on several heterogeneous datasets and show its high discriminative power. Our approach achieves state-of-the-art performance and even beyond in much less time than alternative approaches. Thereby, it facilitates the topological analysis of large-scale data sets in future.

Persistence Codebooks for Topological Data Analysis

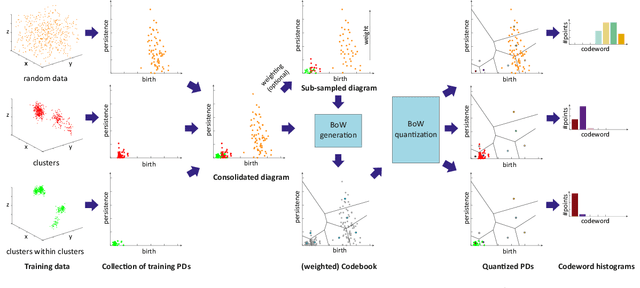
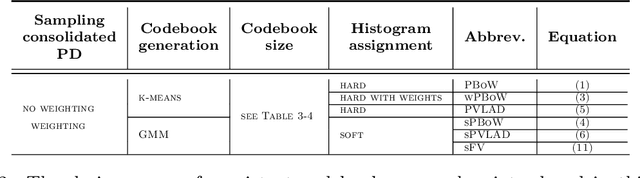
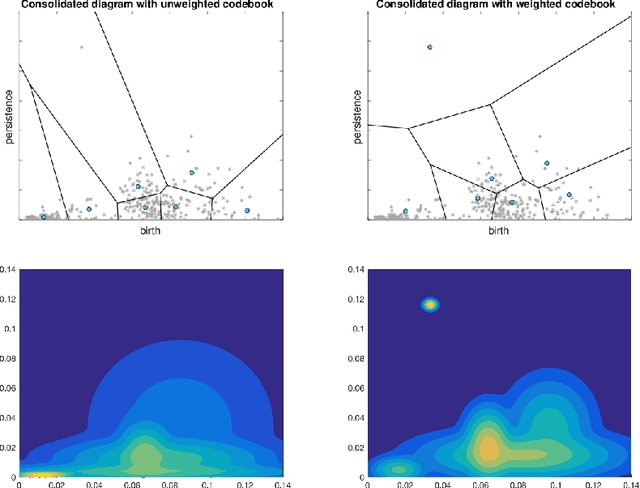
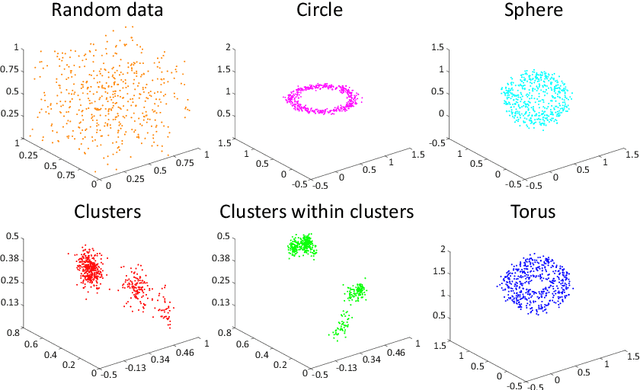
Topological data analysis, such as persistent homology has shown beneficial properties for machine learning in many tasks. Topological representations, such as the persistence diagram (PD), however, have a complex structure (multiset of intervals) which makes it difficult to combine with typical machine learning workflows. We present novel compact fixed-size vectorial representations of PDs based on clustering and bag of words encodings that cope well with the inherent sparsity of PDs. Our novel representations outperform state-of-the-art approaches from topological data analysis and are computationally more efficient.

A Study on Topological Descriptors for the Analysis of 3D Surface Texture

Methods from computational topology are becoming more and more popular in computer vision and have shown to improve the state-of-the-art in several tasks. In this paper, we investigate the applicability of topological descriptors in the context of 3D surface analysis for the classification of different surface textures. We present a comprehensive study on topological descriptors, investigate their robustness and expressiveness and compare them with state-of-the-art methods including Convolutional Neural Networks (CNNs). Results show that class-specific information is reflected well in topological descriptors. The investigated descriptors can directly compete with non-topological descriptors and capture complementary information. As a consequence they improve the state-of-the-art when combined with non-topological descriptors.

Topological descriptors for 3D surface analysis

We investigate topological descriptors for 3D surface analysis, i.e. the classification of surfaces according to their geometric fine structure. On a dataset of high-resolution 3D surface reconstructions we compute persistence diagrams for a 2D cubical filtration. In the next step we investigate different topological descriptors and measure their ability to discriminate structurally different 3D surface patches. We evaluate their sensitivity to different parameters and compare the performance of the resulting topological descriptors to alternative (non-topological) descriptors. We present a comprehensive evaluation that shows that topological descriptors are (i) robust, (ii) yield state-of-the-art performance for the task of 3D surface analysis and (iii) improve classification performance when combined with non-topological descriptors.