Persistence Bag-of-Words for Topological Data Analysis

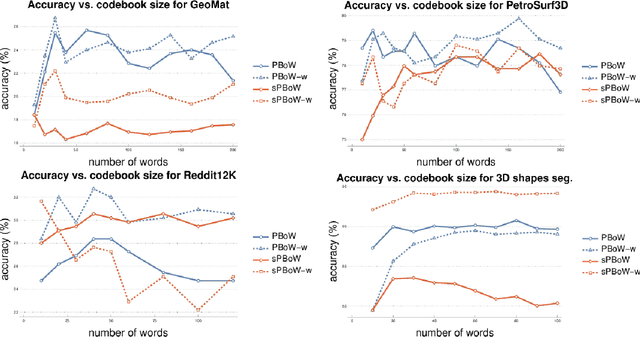
Persistent homology (PH) is a rigorous mathematical theory that provides a robust descriptor of data in the form of persistence diagrams (PDs). PDs are compact 2D representations formed by multisets of points. Their variable size makes them, however, difficult to combine with typical machine learning workflows. In this paper, we introduce persistence bag-of-words, which is a novel, expressive and discriminative vectorized representation of PDs for topological data analysis. It represents PDs in a convenient way for machine learning and statistical analysis and has a number of favorable practical and theoretical properties like 1-Wasserstein stability. We evaluate our representation on several heterogeneous datasets and show its high discriminative power. Our approach achieves state-of-the-art performance and even beyond in much less time than alternative approaches. Thereby, it facilitates the topological analysis of large-scale data sets in future.