ClusterGraph: a new tool for visualization and compression of multidimensional data

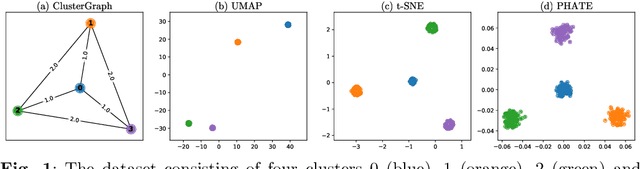
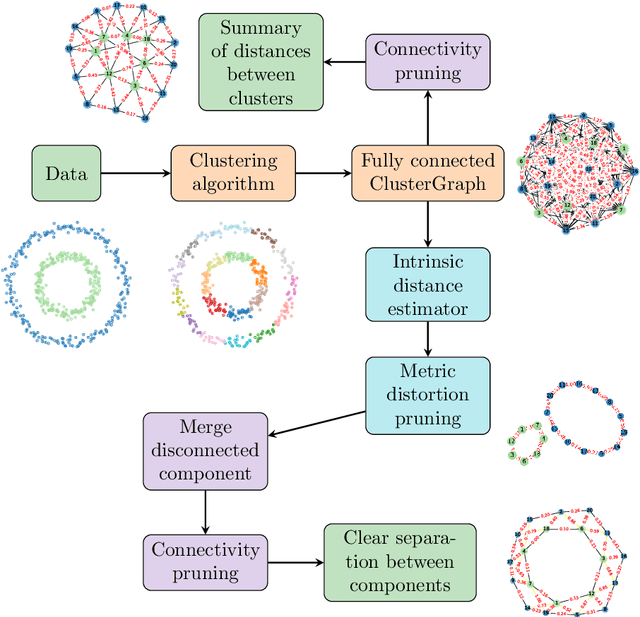
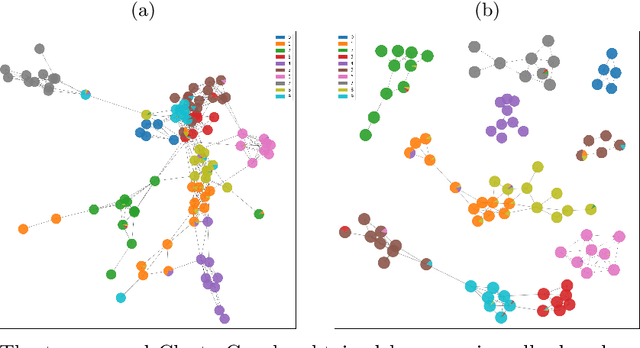
Understanding the global organization of complicated and high dimensional data is of primary interest for many branches of applied sciences. It is typically achieved by applying dimensionality reduction techniques mapping the considered data into lower dimensional space. This family of methods, while preserving local structures and features, often misses the global structure of the dataset. Clustering techniques are another class of methods operating on the data in the ambient space. They group together points that are similar according to a fixed similarity criteria, however unlike dimensionality reduction techniques, they do not provide information about the global organization of the data. Leveraging ideas from Topological Data Analysis, in this paper we provide an additional layer on the output of any clustering algorithm. Such data structure, ClusterGraph, provides information about the global layout of clusters, obtained from the considered clustering algorithm. Appropriate measures are provided to assess the quality and usefulness of the obtained representation. Subsequently the ClusterGraph, possibly with an appropriate structure--preserving simplification, can be visualized and used in synergy with state of the art exploratory data analysis techniques.

Euler Characteristic Curves and Profiles: a stable shape invariant for big data problems

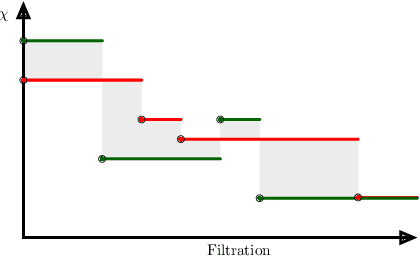
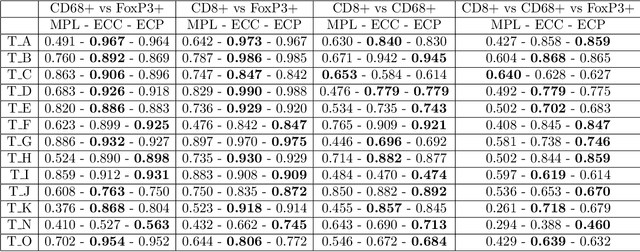
Tools of Topological Data Analysis provide stable summaries encapsulating the shape of the considered data. Persistent homology, the most standard and well studied data summary, suffers a number of limitations; its computations are hard to distribute, it is hard to generalize to multifiltrations and is computationally prohibitive for big data-sets. In this paper we study the concept of Euler Characteristics Curves, for one parameter filtrations and Euler Characteristic Profiles, for multi-parameter filtrations. While being a weaker invariant in one dimension, we show that Euler Characteristic based approaches do not possess some handicaps of persistent homology; we show efficient algorithms to compute them in a distributed way, their generalization to multifiltrations and practical applicability for big data problems. In addition we show that the Euler Curves and Profiles enjoys certain type of stability which makes them robust tool in data analysis. Lastly, to show their practical applicability, multiple use-cases are considered.

Knot invariants and their relations: a topological perspective

This work brings methods from topological data analysis to knot theory and develops new data analysis tools inspired by this application. We explore a vast collection of knot invariants and relations between then using Mapper and Ball Mapper algorithms. In particular, we develop versions of the Ball Mapper algorithm that incorporate symmetries and other relations within the data, and provide ways to compare data arising from different descriptors, such as knot invariants. Additionally, we extend the Mapper construction to the case where the range of the lens function is high dimensional rather than a 1-dimensional space, that also provides ways of visualizing functions between high-dimensional spaces. We illustrate the use of these techniques on knot theory data and draw attention to potential implications of our findings in knot theory.