Knot invariants and their relations: a topological perspective

This work brings methods from topological data analysis to knot theory and develops new data analysis tools inspired by this application. We explore a vast collection of knot invariants and relations between then using Mapper and Ball Mapper algorithms. In particular, we develop versions of the Ball Mapper algorithm that incorporate symmetries and other relations within the data, and provide ways to compare data arising from different descriptors, such as knot invariants. Additionally, we extend the Mapper construction to the case where the range of the lens function is high dimensional rather than a 1-dimensional space, that also provides ways of visualizing functions between high-dimensional spaces. We illustrate the use of these techniques on knot theory data and draw attention to potential implications of our findings in knot theory.

Big Data Approaches to Knot Theory: Understanding the Structure of the Jones Polynomial

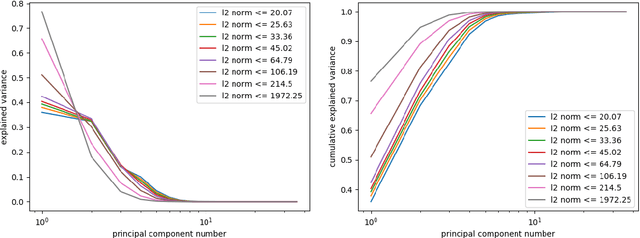
We examine the structure and dimensionality of the Jones polynomial using manifold learning techniques. Our data set consists of more than 10 million knots up to 17 crossings and two other special families up to 2001 crossings. We introduce and describe a method for using filtrations to analyze infinite data sets where representative sampling is impossible or impractical, an essential requirement for working with knots and the data from knot invariants. In particular, this method provides a new approach for analyzing knot invariants using Principal Component Analysis. Using this approach on the Jones polynomial data we find that it can be viewed as an approximately 3 dimensional manifold, that this description is surprisingly stable with respect to the filtration by the crossing number, and that the results suggest further structures to be examined and understood.