Big Data Approaches to Knot Theory: Understanding the Structure of the Jones Polynomial
Paper and Code
Dec 20, 2019

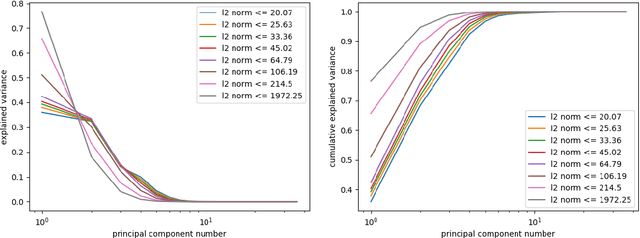
We examine the structure and dimensionality of the Jones polynomial using manifold learning techniques. Our data set consists of more than 10 million knots up to 17 crossings and two other special families up to 2001 crossings. We introduce and describe a method for using filtrations to analyze infinite data sets where representative sampling is impossible or impractical, an essential requirement for working with knots and the data from knot invariants. In particular, this method provides a new approach for analyzing knot invariants using Principal Component Analysis. Using this approach on the Jones polynomial data we find that it can be viewed as an approximately 3 dimensional manifold, that this description is surprisingly stable with respect to the filtration by the crossing number, and that the results suggest further structures to be examined and understood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge