Fitting a deeply-nested hierarchical model to a large book review dataset using a moment-based estimator

We consider a particular instance of a common problem in recommender systems: using a database of book reviews to inform user-targeted recommendations. In our dataset, books are categorized into genres and sub-genres. To exploit this nested taxonomy, we use a hierarchical model that enables information pooling across across similar items at many levels within the genre hierarchy. The main challenge in deploying this model is computational: the data sizes are large, and fitting the model at scale using off-the-shelf maximum likelihood procedures is prohibitive. To get around this computational bottleneck, we extend a moment-based fitting procedure proposed for fitting single-level hierarchical models to the general case of arbitrarily deep hierarchies. This extension is an order of magnetite faster than standard maximum likelihood procedures. The fitting method can be deployed beyond recommender systems to general contexts with deeply-nested hierarchical generalized linear mixed models.

Scaling Text with the Class Affinity Model

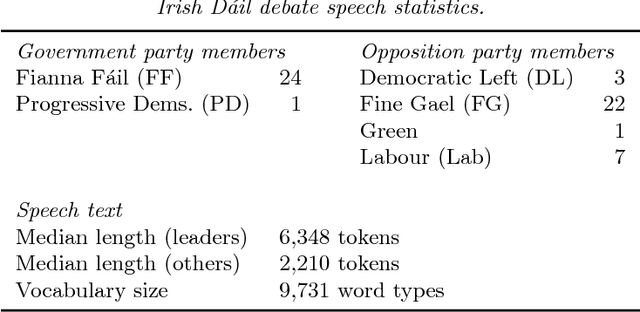
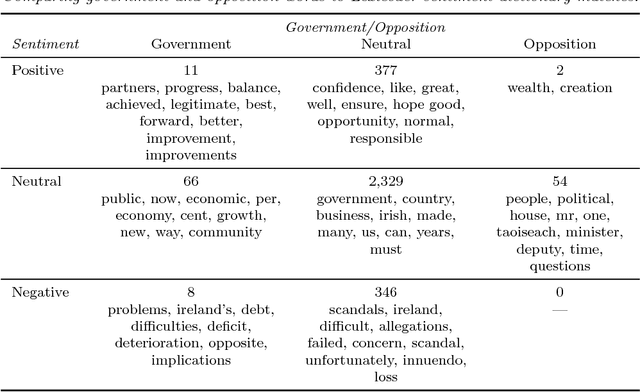
Probabilistic methods for classifying text form a rich tradition in machine learning and natural language processing. For many important problems, however, class prediction is uninteresting because the class is known, and instead the focus shifts to estimating latent quantities related to the text, such as affect or ideology. We focus on one such problem of interest, estimating the ideological positions of 55 Irish legislators in the 1991 D\'ail confidence vote. To solve the D\'ail scaling problem and others like it, we develop a text modeling framework that allows actors to take latent positions on a "gray" spectrum between "black" and "white" polar opposites. We are able to validate results from this model by measuring the influences exhibited by individual words, and we are able to quantify the uncertainty in the scaling estimates by using a sentence-level block bootstrap. Applying our method to the D\'ail debate, we are able to scale the legislators between extreme pro-government and pro-opposition in a way that reveals nuances in their speeches not captured by their votes or party affiliations.

Consistent Biclustering

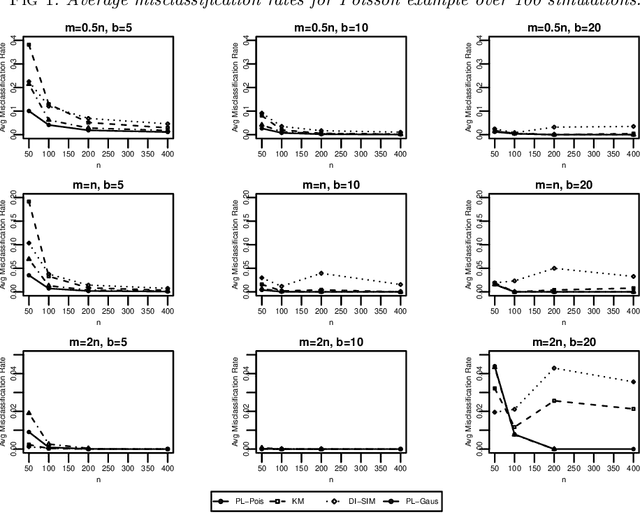
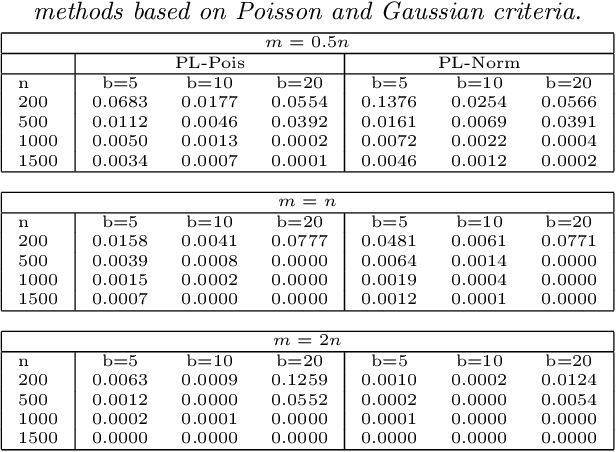
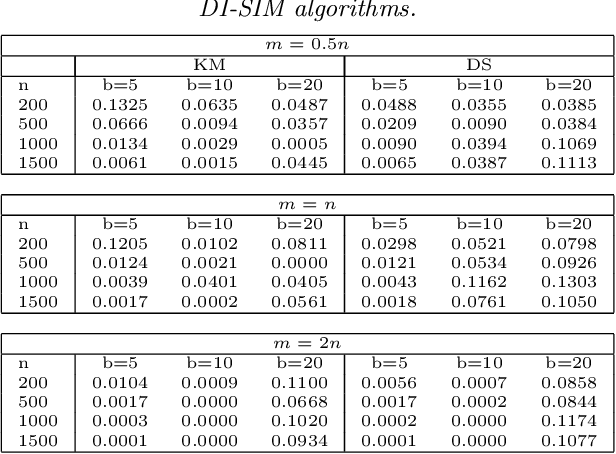
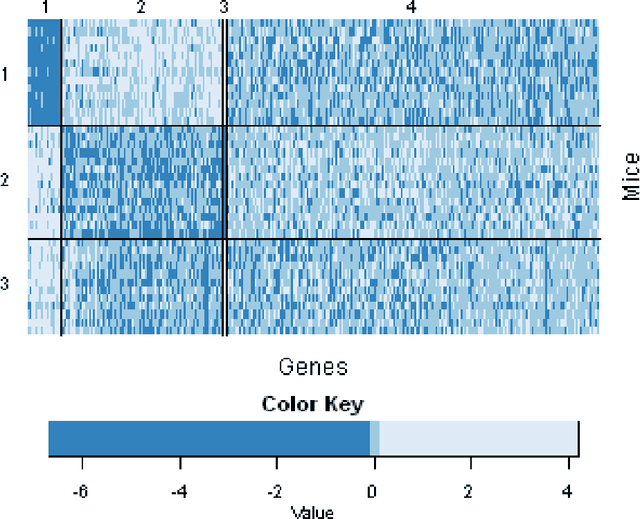
Biclustering, the process of simultaneously clustering the rows and columns of a data matrix, is a popular and effective tool for finding structure in a high-dimensional dataset. Many biclustering procedures appear to work well in practice, but most do not have associated consistency guarantees. To address this shortcoming, we propose a new biclustering procedure based on profile likelihood. The procedure applies to a broad range of data modalities, including binary, count, and continuous observations. We prove that the procedure recovers the true row and column classes when the dimensions of the data matrix tend to infinity, even if the functional form of the data distribution is misspecified. The procedure requires computing a combinatorial search, which can be expensive in practice. Rather than performing this search directly, we propose a new heuristic optimization procedure based on the Kernighan-Lin heuristic, which has nice computational properties and performs well in simulations. We demonstrate our procedure with applications to congressional voting records, and microarray analysis.

Regularized Laplacian Estimation and Fast Eigenvector Approximation

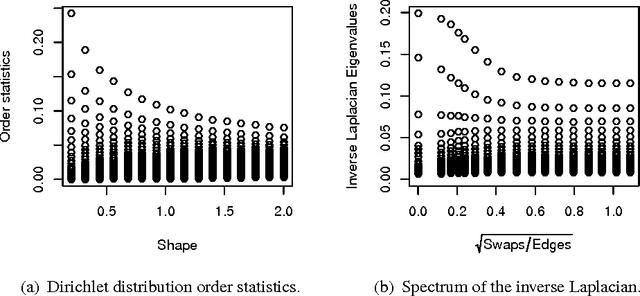
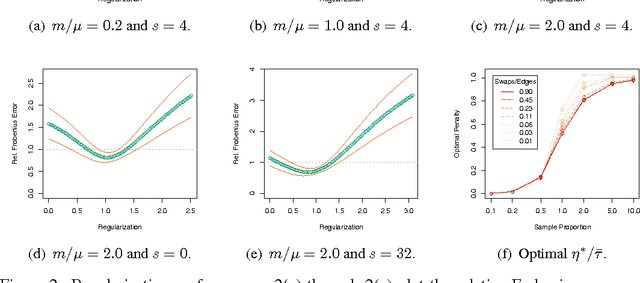
Recently, Mahoney and Orecchia demonstrated that popular diffusion-based procedures to compute a quick \emph{approximation} to the first nontrivial eigenvector of a data graph Laplacian \emph{exactly} solve certain regularized Semi-Definite Programs (SDPs). In this paper, we extend that result by providing a statistical interpretation of their approximation procedure. Our interpretation will be analogous to the manner in which $\ell_2$-regularized or $\ell_1$-regularized $\ell_2$-regression (often called Ridge regression and Lasso regression, respectively) can be interpreted in terms of a Gaussian prior or a Laplace prior, respectively, on the coefficient vector of the regression problem. Our framework will imply that the solutions to the Mahoney-Orecchia regularized SDP can be interpreted as regularized estimates of the pseudoinverse of the graph Laplacian. Conversely, it will imply that the solution to this regularized estimation problem can be computed very quickly by running, e.g., the fast diffusion-based PageRank procedure for computing an approximation to the first nontrivial eigenvector of the graph Laplacian. Empirical results are also provided to illustrate the manner in which approximate eigenvector computation \emph{implicitly} performs statistical regularization, relative to running the corresponding exact algorithm.