Consistent Biclustering
Paper and Code
Jan 08, 2016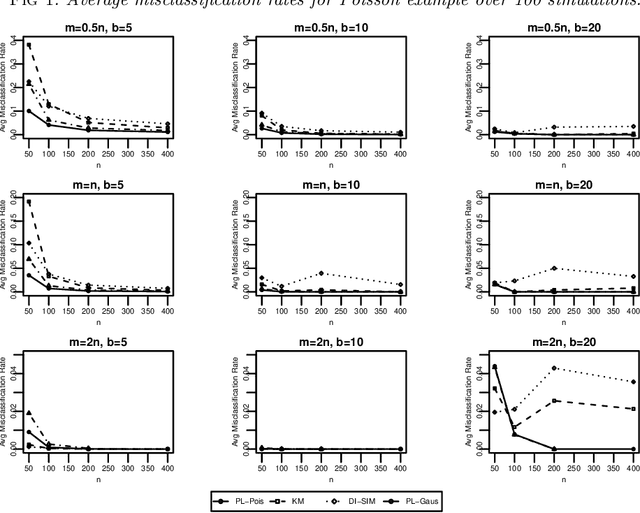
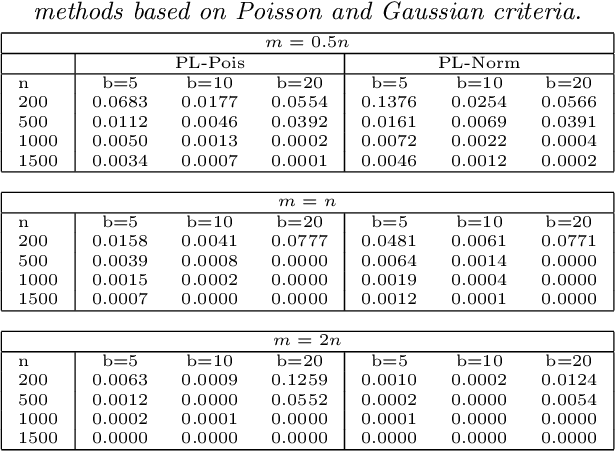
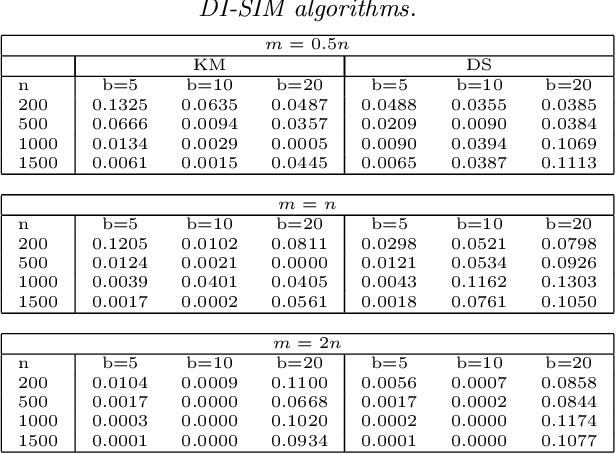
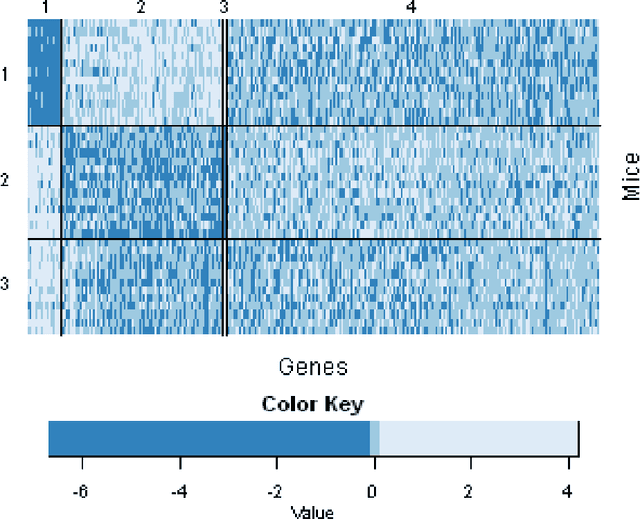
Biclustering, the process of simultaneously clustering the rows and columns of a data matrix, is a popular and effective tool for finding structure in a high-dimensional dataset. Many biclustering procedures appear to work well in practice, but most do not have associated consistency guarantees. To address this shortcoming, we propose a new biclustering procedure based on profile likelihood. The procedure applies to a broad range of data modalities, including binary, count, and continuous observations. We prove that the procedure recovers the true row and column classes when the dimensions of the data matrix tend to infinity, even if the functional form of the data distribution is misspecified. The procedure requires computing a combinatorial search, which can be expensive in practice. Rather than performing this search directly, we propose a new heuristic optimization procedure based on the Kernighan-Lin heuristic, which has nice computational properties and performs well in simulations. We demonstrate our procedure with applications to congressional voting records, and microarray analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge