Two-layer Near-lossless HDR Coding with Backward Compatibility to JPEG

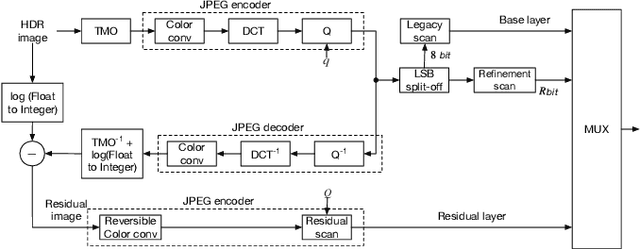
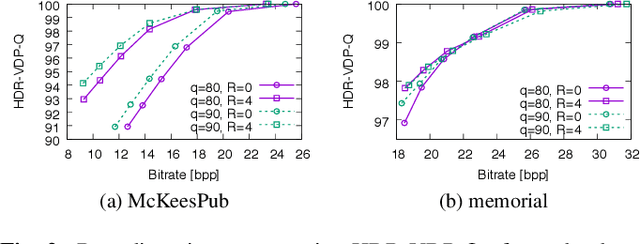
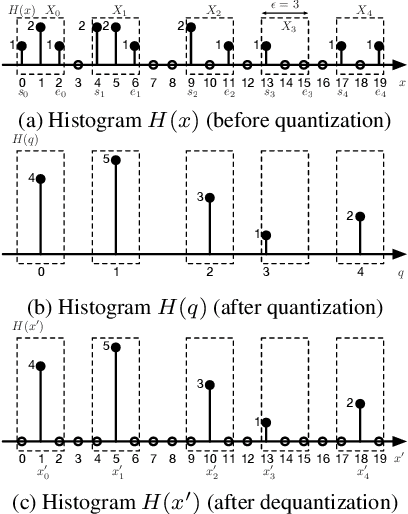
We propose an efficient two-layer near-lossless coding method using an extended histogram packing technique with backward compatibility to the legacy JPEG standard. The JPEG XT, which is the international standard to compress HDR images, adopts a two-layer coding method for backward compatibility to the legacy JPEG standard. However, there are two problems with this two-layer coding method. One is that it does not exhibit better near-lossless performance than other methods for HDR image compression with single-layer structure. The other problem is that the determining the appropriate values of the coding parameters may be required for each input image to achieve good compression performance of near-lossless compression with the two-layer coding method of the JPEG XT. To solve these problems, we focus on a histogram-packing technique that takes into account the histogram sparseness of HDR images. We used zero-skip quantization, which is an extension of the histogram-packing technique proposed for lossless coding, for implementing the proposed near-lossless coding method. The experimental results indicate that the proposed method exhibits not only a better near-lossless compression performance than that of the two-layer coding method of the JPEG XT, but also there are no issue regarding the combination of parameter values without losing backward compatibility to the JPEG standard.

Two-Layer Lossless HDR Coding using Histogram Packing Technique with Backward Compatibility to JPEG

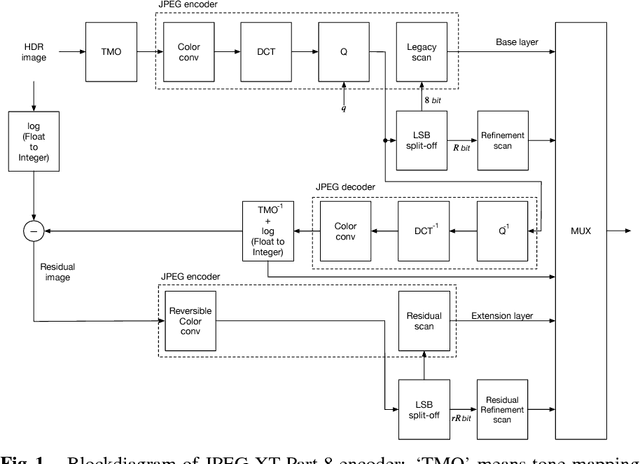
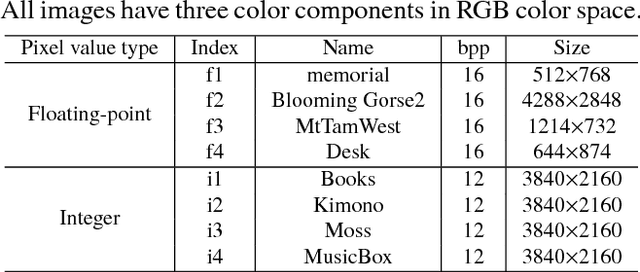
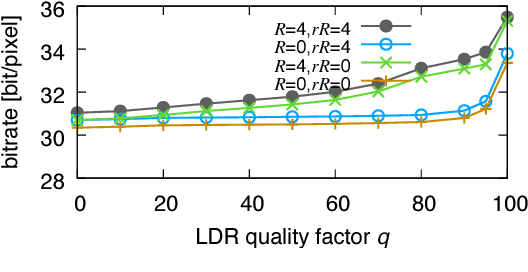
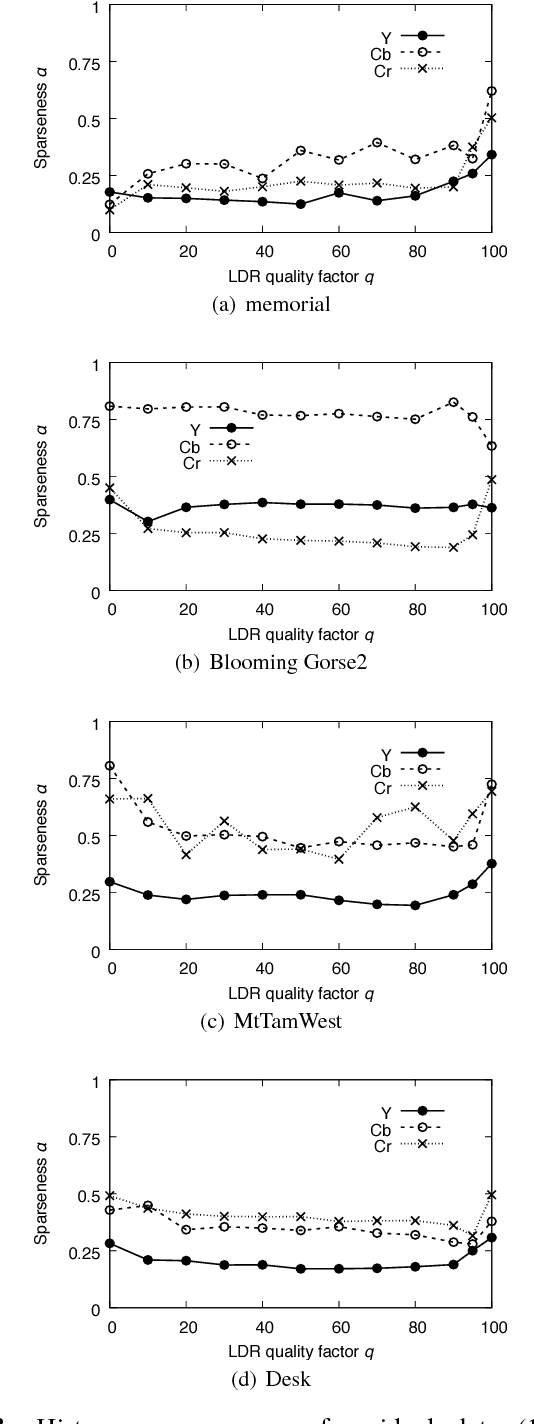
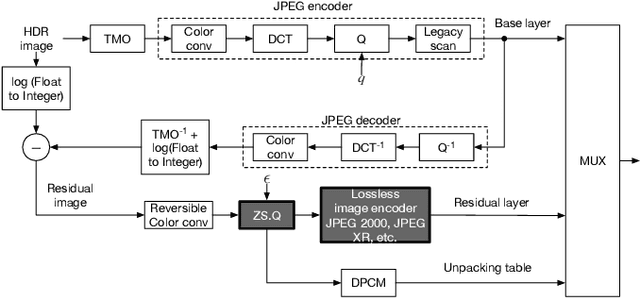
An efficient two-layer coding method using the histogram packing technique with the backward compatibility to the legacy JPEG is proposed in this paper. The JPEG XT, which is the international standard to compress HDR images, adopts two-layer coding scheme for backward compatibility to the legacy JPEG. However, this two-layer coding structure does not give better lossless performance than the other existing methods for HDR image compression with single-layer structure. Moreover, the lossless compression of the JPEG XT has a problem on determination of the coding parameters; The lossless performance is affected by the input images and/or the parameter values. That is, finding appropriate combination of the values is necessary to achieve good lossless performance. It is firstly pointed out that the histogram packing technique considering the histogram sparseness of HDR images is able to improve the performance of lossless compression. Then, a novel two-layer coding with the histogram packing technique and an additional lossless encoder is proposed. The experimental results demonstrate that not only the proposed method has a better lossless compression performance than that of the JPEG XT, but also there is no need to determine image-dependent parameter values for good compression performance without losing the backward compatibility to the well known legacy JPEG standard.

Two-layer Lossless HDR Coding considering Histogram Sparseness with Backward Compatibility to JPEG

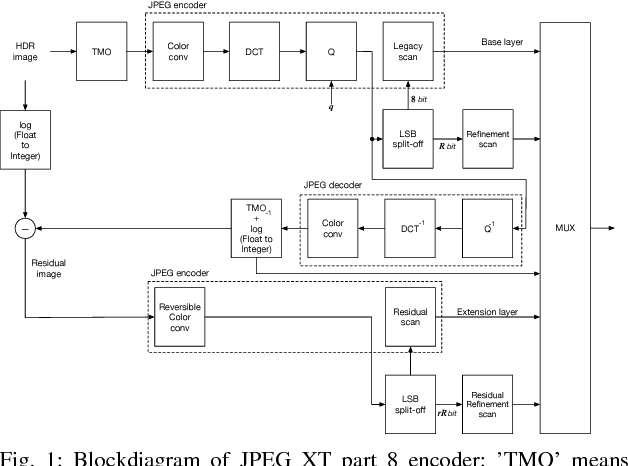
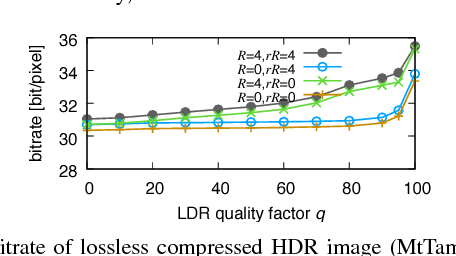
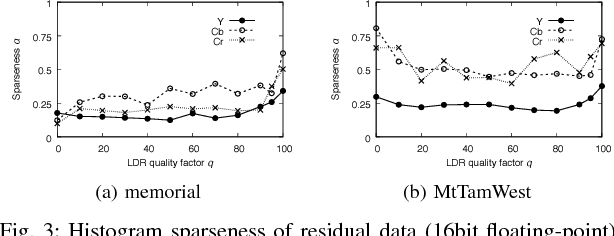
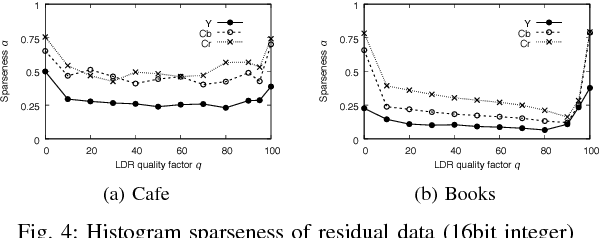
An efficient two-layer coding method using the histogram packing technique with the backward compatibility to the legacy JPEG is proposed in this paper. The JPEG XT, which is the international standard to compress HDR images, adopts two-layer coding scheme for backward compatibility to the legacy JPEG. However, this two-layer coding structure does not give better lossless performance than the other existing single-layer coding methods for HDR images. Moreover, the JPEG XT has problems on determination of the lossless coding parameters; Finding appropriate combination of the parameter values is necessary to achieve good lossless performance. The histogram sparseness of HDR images is discussed and it is pointed out that the histogram packing technique considering the sparseness is able to improve the performance of lossless compression for HDR images and a novel two-layer coding with the histogram packing technique is proposed. The experimental results demonstrate that not only the proposed method has a better lossless compression performance than that of the JPEG XT, but also there is no need to determine image-dependent parameter values for good compression performance in spite of having the backward compatibility to the well known legacy JPEG standard.

Generalized Shortest Path Kernel on Graphs

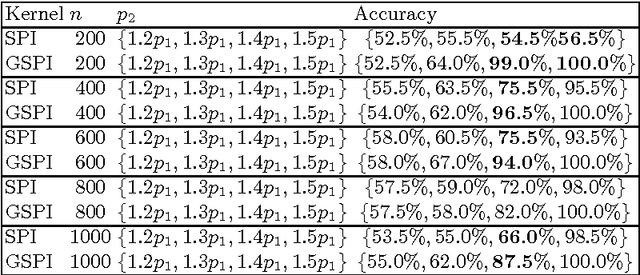
We consider the problem of classifying graphs using graph kernels. We define a new graph kernel, called the generalized shortest path kernel, based on the number and length of shortest paths between nodes. For our example classification problem, we consider the task of classifying random graphs from two well-known families, by the number of clusters they contain. We verify empirically that the generalized shortest path kernel outperforms the original shortest path kernel on a number of datasets. We give a theoretical analysis for explaining our experimental results. In particular, we estimate distributions of the expected feature vectors for the shortest path kernel and the generalized shortest path kernel, and we show some evidence explaining why our graph kernel outperforms the shortest path kernel for our graph classification problem.

A role of constraint in self-organization

In this paper we introduce a neural network model of self-organization. This model uses a variation of Hebb rule for updating its synaptic weights, and surely converges to the equilibrium status. The key point of the convergence is the update rule that constrains the total synaptic weight and this seems to make the model stable. We investigate the role of the constraint and show that it is the constraint that makes the model stable. For analyzing this setting, we propose a simple probabilistic game that models the neural network and the self-organization process. Then, we investigate the characteristics of this game, namely, the probability that the game becomes stable and the number of the steps it takes.

Practical algorithms for on-line sampling

One of the core applications of machine learning to knowledge discovery consists on building a function (a hypothesis) from a given amount of data (for instance a decision tree or a neural network) such that we can use it afterwards to predict new instances of the data. In this paper, we focus on a particular situation where we assume that the hypothesis we want to use for prediction is very simple, and thus, the hypotheses class is of feasible size. We study the problem of how to determine which of the hypotheses in the class is almost the best one. We present two on-line sampling algorithms for selecting hypotheses, give theoretical bounds on the number of necessary examples, and analize them exprimentally. We compare them with the simple batch sampling approach commonly used and show that in most of the situations our algorithms use much fewer number of examples.