2.5D Super-Resolution Approaches for X-ray Computed Tomography-based Inspection of Additively Manufactured Parts

X-ray computed tomography (XCT) is a key tool in non-destructive evaluation of additively manufactured (AM) parts, allowing for internal inspection and defect detection. Despite its widespread use, obtaining high-resolution CT scans can be extremely time consuming. This issue can be mitigated by performing scans at lower resolutions; however, reducing the resolution compromises spatial detail, limiting the accuracy of defect detection. Super-resolution algorithms offer a promising solution for overcoming resolution limitations in XCT reconstructions of AM parts, enabling more accurate detection of defects. While 2D super-resolution methods have demonstrated state-of-the-art performance on natural images, they tend to under-perform when directly applied to XCT slices. On the other hand, 3D super-resolution methods are computationally expensive, making them infeasible for large-scale applications. To address these challenges, we propose a 2.5D super-resolution approach tailored for XCT of AM parts. Our method enhances the resolution of individual slices by leveraging multi-slice information from neighboring 2D slices without the significant computational overhead of full 3D methods. Specifically, we use neighboring low-resolution slices to super-resolve the center slice, exploiting inter-slice spatial context while maintaining computational efficiency. This approach bridges the gap between 2D and 3D methods, offering a practical solution for high-throughput defect detection in AM parts.

Direct Iterative Reconstruction of Multiple Basis Material Images in Photon-counting Spectral CT

In this work, we perform direct material reconstruction from spectral CT data using a model based iterative reconstruction (MBIR) approach. Material concentrations are measured in volume fractions, whose total is constrained by a maximum of unity. A phantom containing a combination of 4 basis materials (water, iodine, gadolinium, calcium) was scanned using a photon-counting detector. Iodine and gadolinium were chosen because of their common use as contrast agents in CT imaging. Scan data was binned into 5 energy (keV) levels. Each energy bin in a calibration scan was reconstructed, allowing the linear attenuation coefficient of each material for every energy to be estimated by a least-squares fit to ground truth in the image domain. The resulting $5\times 4$ matrix, for $5$ energies and $4$ materials, is incorporated into the forward model in direct reconstruction of the $4$ basis material images with spatial and/or inter-material regularization. In reconstruction from a subsequent low-concentration scan, volume fractions within regions of interest (ROIs) are found to be close to the ground truth. This work is meant to lay the foundation for further work with phantoms including spatially coincident mixtures of contrast materials and/or contrast agents in widely varying concentrations, molecular imaging from animal scans, and eventually clinical applications.

Deep learning based workflow for accelerated industrial X-ray Computed Tomography

X-ray computed tomography (XCT) is an important tool for high-resolution non-destructive characterization of additively-manufactured metal components. XCT reconstructions of metal components may have beam hardening artifacts such as cupping and streaking which makes reliable detection of flaws and defects challenging. Furthermore, traditional workflows based on using analytic reconstruction algorithms require a large number of projections for accurate characterization - leading to longer measurement times and hindering the adoption of XCT for in-line inspections. In this paper, we introduce a new workflow based on the use of two neural networks to obtain high-quality accelerated reconstructions from sparse-view XCT scans of single material metal parts. The first network, implemented using fully-connected layers, helps reduce the impact of BH in the projection data without the need of any calibration or knowledge of the component material. The second network, a convolutional neural network, maps a low-quality analytic 3D reconstruction to a high-quality reconstruction. Using experimental data, we demonstrate that our method robustly generalizes across several alloys, and for a range of sparsity levels without any need for retraining the networks thereby enabling accurate and fast industrial XCT inspections.

Design of Novel Loss Functions for Deep Learning in X-ray CT

Deep learning (DL) shows promise of advantages over conventional signal processing techniques in a variety of imaging applications. The networks' being trained from examples of data rather than explicitly designed allows them to learn signal and noise characteristics to most effectively construct a mapping from corrupted data to higher quality representations. In inverse problems, one has options of applying DL in the domain of the originally captured data, in the transformed domain of the desired final representation, or both. X-ray computed tomography (CT), one of the most valuable tools in medical diagnostics, is already being improved by DL methods. Whether for removal of common quantum noise resulting from the Poisson-distributed photon counts, or for reduction of the ill effects of metal implants on image quality, researchers have begun employing DL widely in CT. The selection of training data is driven quite directly by the corruption on which the focus lies. However, the way in which differences between the target signal and measured data is penalized in training generally follows conventional, pointwise loss functions. This work introduces a creative technique for favoring reconstruction characteristics that are not well described by norms such as mean-squared or mean-absolute error. Particularly in a field such as X-ray CT, where radiologists' subjective preferences in image characteristics are key to acceptance, it may be desirable to penalize differences in DL more creatively. This penalty may be applied in the data domain, here the CT sinogram, or in the reconstructed image. We design loss functions for both shaping and selectively preserving frequency content of the signal.

Statistically Adaptive Filtering for Low Signal Correction in X-ray Computed Tomography

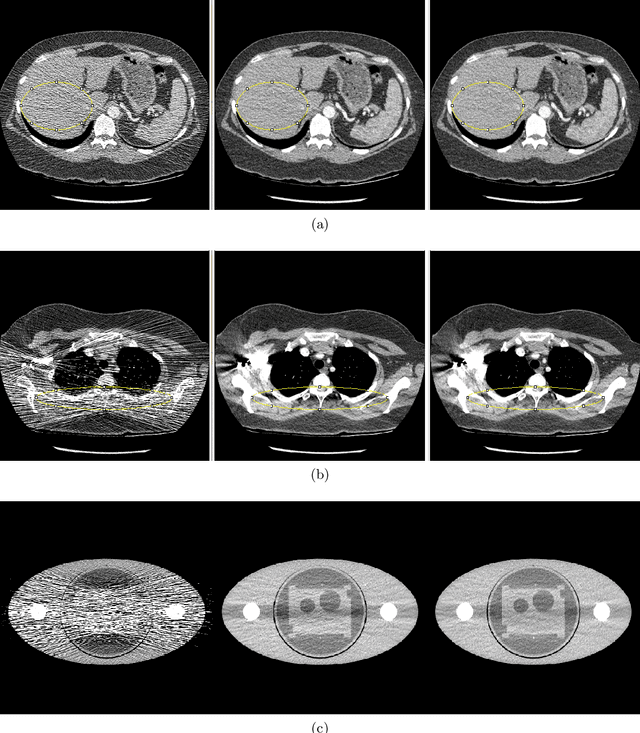
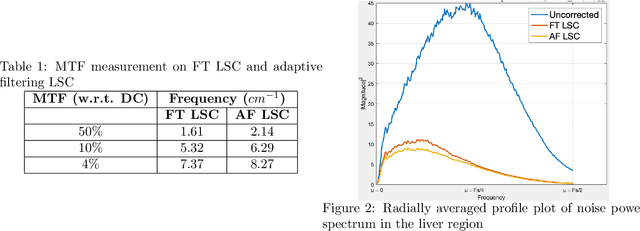
Low x-ray dose is desirable in x-ray computed tomographic (CT) imaging due to health concerns. But low dose comes with a cost of low signal artifacts such as streaks and low frequency bias in the reconstruction. As a result, low signal correction is needed to help reduce artifacts while retaining relevant anatomical structures. Low signal can be encountered in cases where sufficient number of photons do not reach the detector to have confidence in the recorded data. % NOTE: SNR is ratio of powers, not std. dev. X-ray photons, assumed to have Poisson distribution, have signal to noise ratio proportional to the dose, with poorer SNR in low signal areas. Electronic noise added by the data acquisition system further reduces the signal quality. In this paper we will demonstrate a technique to combat low signal artifacts through adaptive filtration. It entails statistics-based filtering on the uncorrected data, correcting the lower signal areas more aggressively than the high signal ones. We look at local averages to decide how aggressive the filtering should be, and local standard deviation to decide how much detail preservation to apply. Implementation consists of a pre-correction step i.e. local linear minimum mean-squared error correction, followed by a variance stabilizing transform, and finally adaptive bilateral filtering. The coefficients of the bilateral filter are computed using local statistics. Results show that improvements were made in terms of low frequency bias, streaks, local average and standard deviation, modulation transfer function and noise power spectrum.

MBIR Training for a 2.5D DL network in X-ray CT

In computed tomographic imaging, model based iterative reconstruction methods have generally shown better image quality than the more traditional, faster filtered backprojection technique. The cost we have to pay is that MBIR is computationally expensive. In this work we train a 2.5D deep learning (DL) network to mimic MBIR quality image. The network is realized by a modified Unet, and trained using clinical FBP and MBIR image pairs. We achieve the quality of MBIR images faster and with a much smaller computation cost. Visually and in terms of noise power spectrum (NPS), DL-MBIR images have texture similar to that of MBIR, with reduced noise power. Image profile plots, NPS plots, standard deviation, etc. suggest that the DL-MBIR images result from a successful emulation of an MBIR operator.