Design of Novel Loss Functions for Deep Learning in X-ray CT

Deep learning (DL) shows promise of advantages over conventional signal processing techniques in a variety of imaging applications. The networks' being trained from examples of data rather than explicitly designed allows them to learn signal and noise characteristics to most effectively construct a mapping from corrupted data to higher quality representations. In inverse problems, one has options of applying DL in the domain of the originally captured data, in the transformed domain of the desired final representation, or both. X-ray computed tomography (CT), one of the most valuable tools in medical diagnostics, is already being improved by DL methods. Whether for removal of common quantum noise resulting from the Poisson-distributed photon counts, or for reduction of the ill effects of metal implants on image quality, researchers have begun employing DL widely in CT. The selection of training data is driven quite directly by the corruption on which the focus lies. However, the way in which differences between the target signal and measured data is penalized in training generally follows conventional, pointwise loss functions. This work introduces a creative technique for favoring reconstruction characteristics that are not well described by norms such as mean-squared or mean-absolute error. Particularly in a field such as X-ray CT, where radiologists' subjective preferences in image characteristics are key to acceptance, it may be desirable to penalize differences in DL more creatively. This penalty may be applied in the data domain, here the CT sinogram, or in the reconstructed image. We design loss functions for both shaping and selectively preserving frequency content of the signal.

MBIR Training for a 2.5D DL network in X-ray CT

In computed tomographic imaging, model based iterative reconstruction methods have generally shown better image quality than the more traditional, faster filtered backprojection technique. The cost we have to pay is that MBIR is computationally expensive. In this work we train a 2.5D deep learning (DL) network to mimic MBIR quality image. The network is realized by a modified Unet, and trained using clinical FBP and MBIR image pairs. We achieve the quality of MBIR images faster and with a much smaller computation cost. Visually and in terms of noise power spectrum (NPS), DL-MBIR images have texture similar to that of MBIR, with reduced noise power. Image profile plots, NPS plots, standard deviation, etc. suggest that the DL-MBIR images result from a successful emulation of an MBIR operator.

Statistically Adaptive Filtering for Low Signal Correction in X-ray Computed Tomography

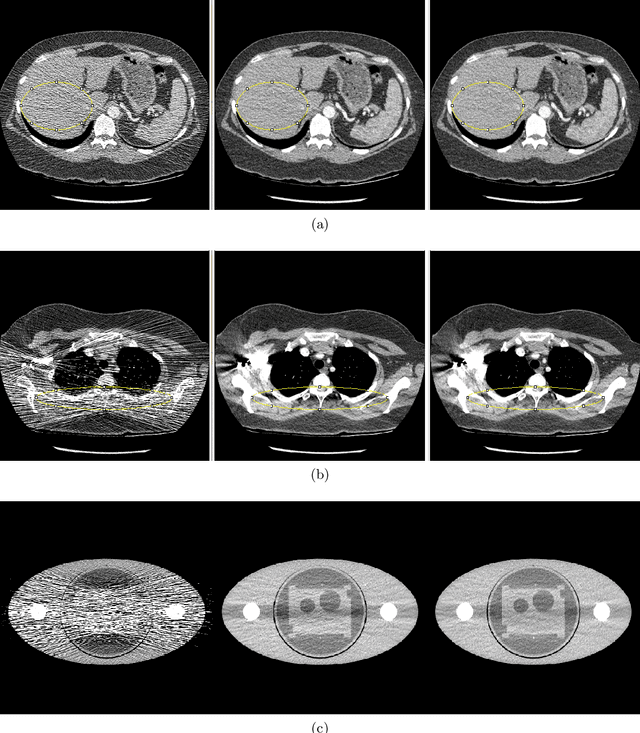
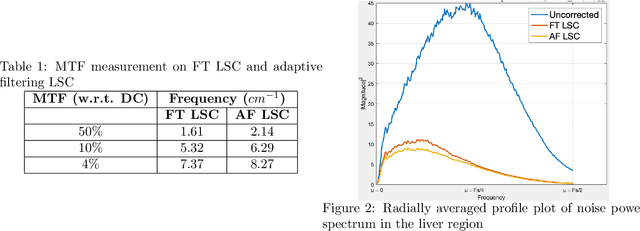
Low x-ray dose is desirable in x-ray computed tomographic (CT) imaging due to health concerns. But low dose comes with a cost of low signal artifacts such as streaks and low frequency bias in the reconstruction. As a result, low signal correction is needed to help reduce artifacts while retaining relevant anatomical structures. Low signal can be encountered in cases where sufficient number of photons do not reach the detector to have confidence in the recorded data. % NOTE: SNR is ratio of powers, not std. dev. X-ray photons, assumed to have Poisson distribution, have signal to noise ratio proportional to the dose, with poorer SNR in low signal areas. Electronic noise added by the data acquisition system further reduces the signal quality. In this paper we will demonstrate a technique to combat low signal artifacts through adaptive filtration. It entails statistics-based filtering on the uncorrected data, correcting the lower signal areas more aggressively than the high signal ones. We look at local averages to decide how aggressive the filtering should be, and local standard deviation to decide how much detail preservation to apply. Implementation consists of a pre-correction step i.e. local linear minimum mean-squared error correction, followed by a variance stabilizing transform, and finally adaptive bilateral filtering. The coefficients of the bilateral filter are computed using local statistics. Results show that improvements were made in terms of low frequency bias, streaks, local average and standard deviation, modulation transfer function and noise power spectrum.