Noman Ahmed Sheikh
PopSkipJump: Decision-Based Attack for Probabilistic Classifiers
Jun 14, 2021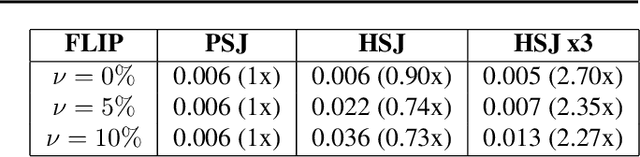
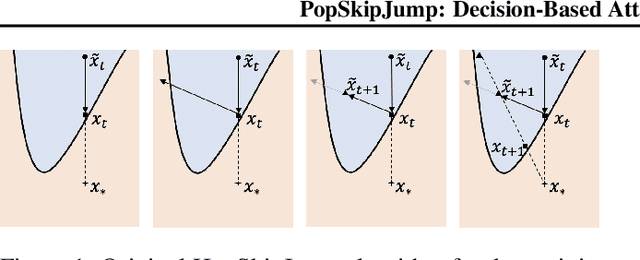
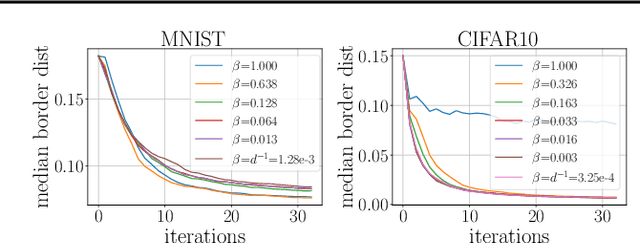

Abstract:Most current classifiers are vulnerable to adversarial examples, small input perturbations that change the classification output. Many existing attack algorithms cover various settings, from white-box to black-box classifiers, but typically assume that the answers are deterministic and often fail when they are not. We therefore propose a new adversarial decision-based attack specifically designed for classifiers with probabilistic outputs. It is based on the HopSkipJump attack by Chen et al. (2019, arXiv:1904.02144v5 ), a strong and query efficient decision-based attack originally designed for deterministic classifiers. Our P(robabilisticH)opSkipJump attack adapts its amount of queries to maintain HopSkipJump's original output quality across various noise levels, while converging to its query efficiency as the noise level decreases. We test our attack on various noise models, including state-of-the-art off-the-shelf randomized defenses, and show that they offer almost no extra robustness to decision-based attacks. Code is available at https://github.com/cjsg/PopSkipJump .
Lifted Marginal MAP Inference
Jul 08, 2018
Abstract:Lifted inference reduces the complexity of inference in relational probabilistic models by identifying groups of constants (or atoms) which behave symmetric to each other. A number of techniques have been proposed in the literature for lifting marginal as well MAP inference. We present the first application of lifting rules for marginal-MAP (MMAP), an important inference problem in models having latent (random) variables. Our main contribution is two fold: (1) we define a new equivalence class of (logical) variables, called Single Occurrence for MAX (SOM), and show that solution lies at extreme with respect to the SOM variables, i.e., predicate groundings differing only in the instantiation of the SOM variables take the same truth value (2) we define a sub-class {\em SOM-R} (SOM Reduce) and exploit properties of extreme assignments to show that MMAP inference can be performed by reducing the domain of SOM-R variables to a single constant.We refer to our lifting technique as the {\em SOM-R} rule for lifted MMAP. Combined with existing rules such as decomposer and binomial, this results in a powerful framework for lifted MMAP. Experiments on three benchmark domains show significant gains in both time and memory compared to ground inference as well as lifted approaches not using SOM-R.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge