Results of the 2023 CommonRoad Motion Planning Competition for Autonomous Vehicles

In recent years, different approaches for motion planning of autonomous vehicles have been proposed that can handle complex traffic situations. However, these approaches are rarely compared on the same set of benchmarks. To address this issue, we present the results of a large-scale motion planning competition for autonomous vehicles based on the CommonRoad benchmark suite. The benchmark scenarios contain highway and urban environments featuring various types of traffic participants, such as passengers, cars, buses, etc. The solutions are evaluated considering efficiency, safety, comfort, and compliance with a selection of traffic rules. This report summarizes the main results of the competition.

Real-Time Capable Decision Making for Autonomous Driving Using Reachable Sets

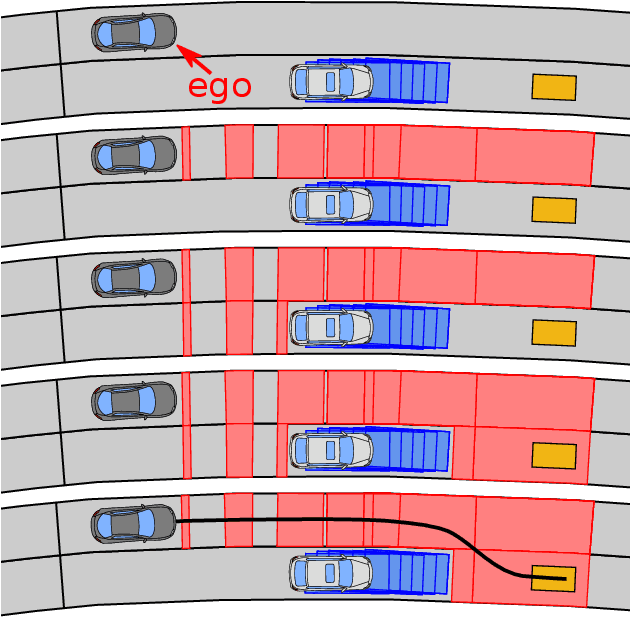
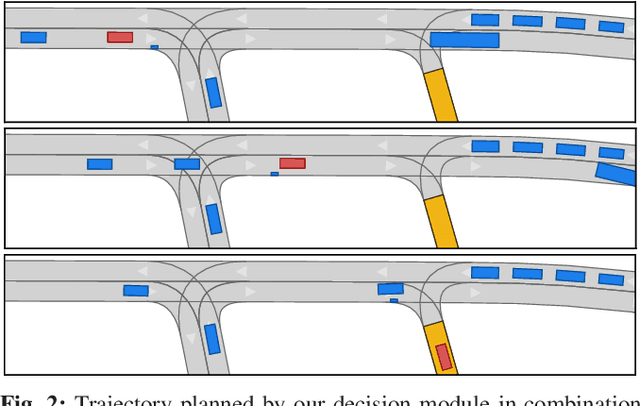
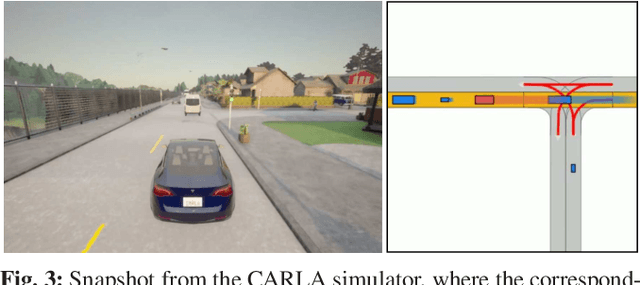
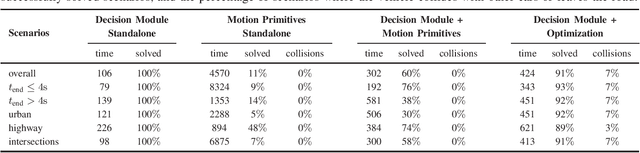
Despite large advances in recent years, real-time capable motion planning for autonomous road vehicles remains a huge challenge. In this work, we present a decision module that is based on set-based reachability analysis: First, we identify all possible driving corridors by computing the reachable set for the longitudinal position of the vehicle along the lanelets of the road network, where lane changes are modeled as discrete events. Next, we select the best driving corridor based on a cost function that penalizes lane changes and deviations from a desired velocity profile. Finally, we generate a reference trajectory inside the selected driving corridor, which can be used to guide or warm start low-level trajectory planners. For the numerical evaluation we combine our decision module with a motion-primitive-based and an optimization-based planner and evaluate the performance on 2000 challenging CommonRoad traffic scenarios as well in the realistic CARLA simulator. The results demonstrate that our decision module is real-time capable and yields significant speed-ups compared to executing a motion planner standalone without a decision module.

Provably Safe Reinforcement Learning via Action Projection using Reachability Analysis and Polynomial Zonotopes

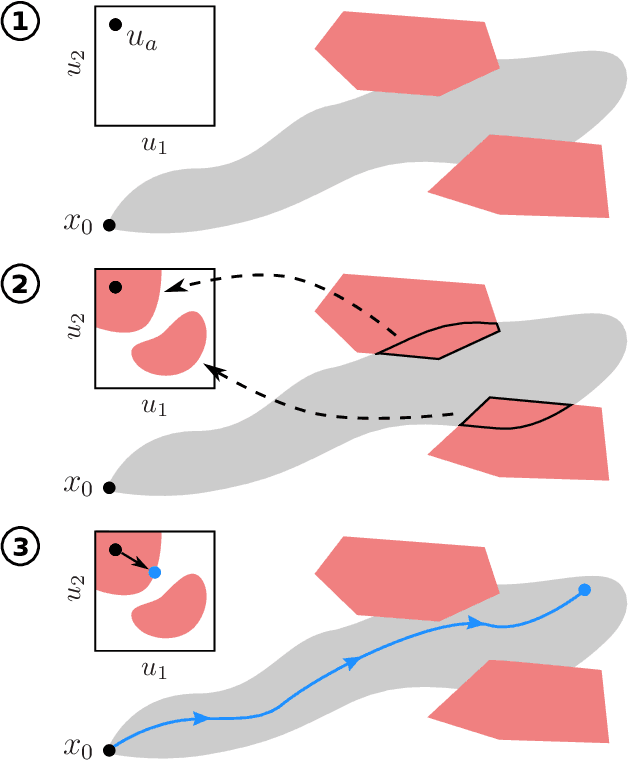
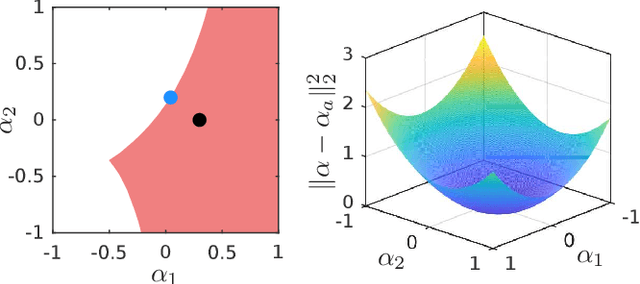
While reinforcement learning produces very promising results for many applications, its main disadvantage is the lack of safety guarantees, which prevents its use in safety-critical systems. In this work, we address this issue by a safety shield for nonlinear continuous systems that solve reach-avoid tasks. Our safety shield prevents applying potentially unsafe actions from a reinforcement learning agent by projecting the proposed action to the closest safe action. This approach is called action projection and is implemented via mixed-integer optimization. The safety constraints for action projection are obtained by applying parameterized reachability analysis using polynomial zonotopes, which enables to accurately capture the nonlinear effects of the actions on the system. In contrast to other state of the art approaches for action projection, our safety shield can efficiently handle input constraints and dynamic obstacles, eases incorporation of the spatial robot dimensions into the safety constraints, guarantees robust safety despite process noise and measurement errors, and is well suited for high-dimensional systems, as we demonstrate on several challenging benchmark systems.

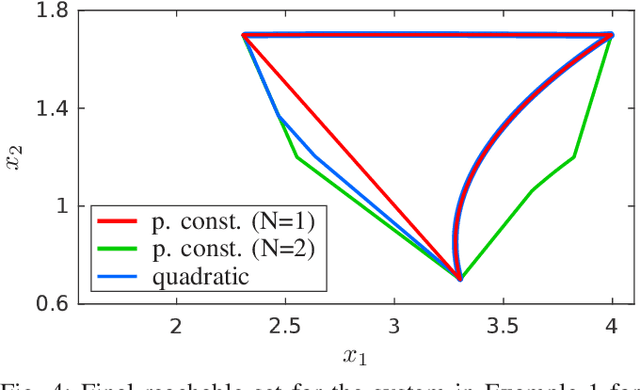
Open- and Closed-Loop Neural Network Verification using Polynomial Zonotopes

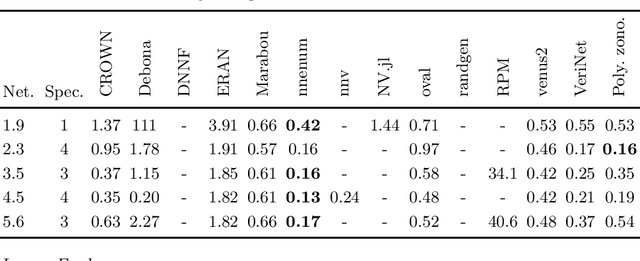
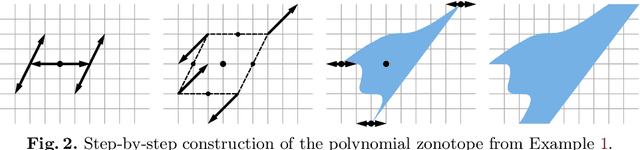
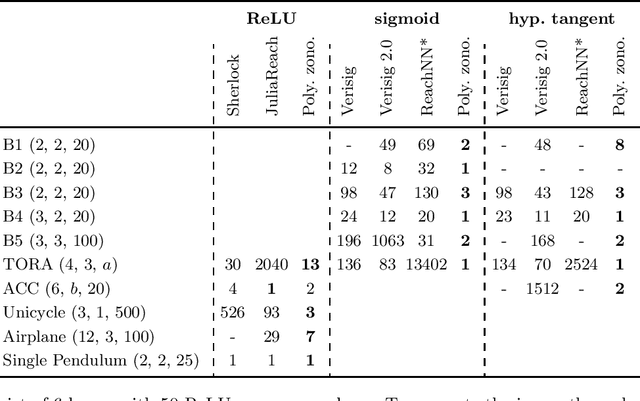
We present a novel approach to efficiently compute tight non-convex enclosures of the image through neural networks with ReLU, sigmoid, or hyperbolic tangent activation functions. In particular, we abstract the input-output relation of each neuron by a polynomial approximation, which is evaluated in a set-based manner using polynomial zonotopes. Our proposed method is especially well suited for reachability analysis of neural network controlled systems since polynomial zonotopes are able to capture the non-convexity in both, the image through the neural network as well as the reachable set. We demonstrate the superior performance of our approach compared to other state of the art methods on various benchmark systems.