Nihesh Anderson
Task Selection for AutoML System Evaluation
Aug 26, 2022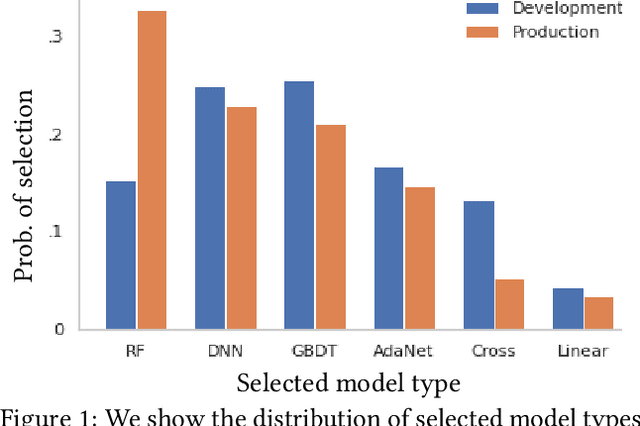

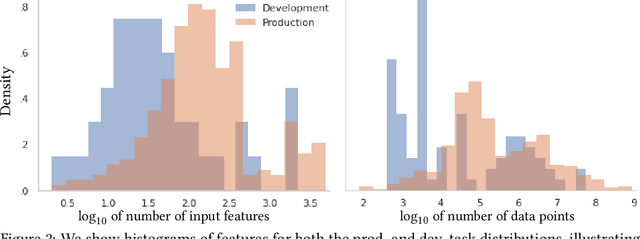

Abstract:Our goal is to assess if AutoML system changes - i.e., to the search space or hyperparameter optimization - will improve the final model's performance on production tasks. However, we cannot test the changes on production tasks. Instead, we only have access to limited descriptors about tasks that our AutoML system previously executed, like the number of data points or features. We also have a set of development tasks to test changes, ex., sampled from OpenML with no usage constraints. However, the development and production task distributions are different leading us to pursue changes that only improve development and not production. This paper proposes a method to leverage descriptor information about AutoML production tasks to select a filtered subset of the most relevant development tasks. Empirical studies show that our filtering strategy improves the ability to assess AutoML system changes on holdout tasks with different distributions than development.
Distributional Individual Fairness in Clustering
Jun 22, 2020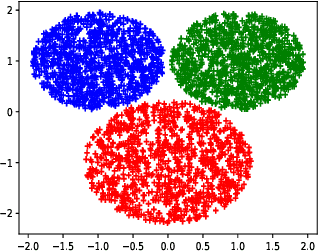

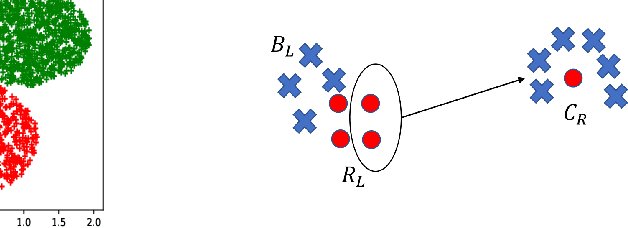

Abstract:In this paper, we initiate the study of fair clustering that ensures distributional similarity among similar individuals. In response to improving fairness in machine learning, recent papers have investigated fairness in clustering algorithms and have focused on the paradigm of statistical parity/group fairness. These efforts attempt to minimize bias against some protected groups in the population. However, to the best of our knowledge, the alternative viewpoint of individual fairness, introduced by Dwork et al. (ITCS 2012) in the context of classification, has not been considered for clustering so far. Similar to Dwork et al., we adopt the individual fairness notion which mandates that similar individuals should be treated similarly for clustering problems. We use the notion of $f$-divergence as a measure of statistical similarity that significantly generalizes the ones used by Dwork et al. We introduce a framework for assigning individuals, embedded in a metric space, to probability distributions over a bounded number of cluster centers. The objective is to ensure (a) low cost of clustering in expectation and (b) individuals that are close to each other in a given fairness space are mapped to statistically similar distributions. We provide an algorithm for clustering with $p$-norm objective ($k$-center, $k$-means are special cases) and individual fairness constraints with provable approximation guarantee. We extend this framework to include both group fairness and individual fairness inside the protected groups. Finally, we observe conditions under which individual fairness implies group fairness. We present extensive experimental evidence that justifies the effectiveness of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge