Distributional Individual Fairness in Clustering

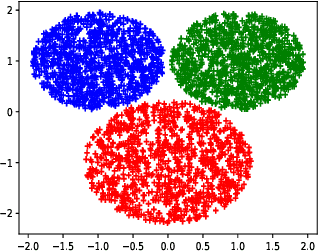
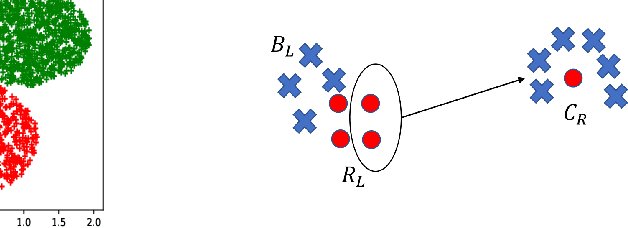
In this paper, we initiate the study of fair clustering that ensures distributional similarity among similar individuals. In response to improving fairness in machine learning, recent papers have investigated fairness in clustering algorithms and have focused on the paradigm of statistical parity/group fairness. These efforts attempt to minimize bias against some protected groups in the population. However, to the best of our knowledge, the alternative viewpoint of individual fairness, introduced by Dwork et al. (ITCS 2012) in the context of classification, has not been considered for clustering so far. Similar to Dwork et al., we adopt the individual fairness notion which mandates that similar individuals should be treated similarly for clustering problems. We use the notion of $f$-divergence as a measure of statistical similarity that significantly generalizes the ones used by Dwork et al. We introduce a framework for assigning individuals, embedded in a metric space, to probability distributions over a bounded number of cluster centers. The objective is to ensure (a) low cost of clustering in expectation and (b) individuals that are close to each other in a given fairness space are mapped to statistically similar distributions. We provide an algorithm for clustering with $p$-norm objective ($k$-center, $k$-means are special cases) and individual fairness constraints with provable approximation guarantee. We extend this framework to include both group fairness and individual fairness inside the protected groups. Finally, we observe conditions under which individual fairness implies group fairness. We present extensive experimental evidence that justifies the effectiveness of our approach.

Fenchel Duals for Drifting Adversaries

We describe a primal-dual framework for the design and analysis of online convex optimization algorithms for {\em drifting regret}. Existing literature shows (nearly) optimal drifting regret bounds only for the $\ell_2$ and the $\ell_1$-norms. Our work provides a connection between these algorithms and the Online Mirror Descent ($\omd$) updates; one key insight that results from our work is that in order for these algorithms to succeed, it suffices to have the gradient of the regularizer to be bounded (in an appropriate norm). For situations (like for the $\ell_1$ norm) where the vanilla regularizer does not have this property, we have to {\em shift} the regularizer to ensure this. Thus, this helps explain the various updates presented in \cite{bansal10, buchbinder12}. We also consider the online variant of the problem with 1-lookahead, and with movement costs in the $\ell_2$-norm. Our primal dual approach yields nearly optimal competitive ratios for this problem.