Robust-by-Design Plans for Multi-Robot Pursuit-Evasion

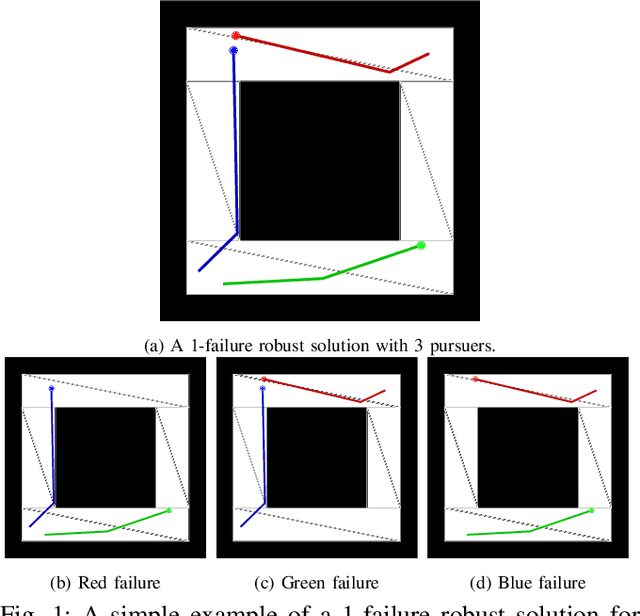
This paper studies a multi-robot visibility-based pursuit-evasion problem in which a group of pursuer robots are tasked with detecting an evader within a two dimensional polygonal environment. The primary contribution is a novel formulation of the pursuit-evasion problem that modifies the pursuers' objective by requiring that the evader still be detected, even in spite of the failure of any single pursuer robot. This novel constraint, whereby two pursuers are required to detect an evader, has the benefit of providing redundancy to the search, should any member of the team become unresponsive, suffer temporary sensor disruption/failure, or otherwise become incapacitated. Existing methods, even those that are designed to respond to failures, rely on the pursuers to replan and update their search pattern to handle such occurrences. In contrast, the proposed formulation produces plans that are inherently tolerant of some level of disturbance. Building upon this new formulation, we introduce an augmented data structure for encoding the problem state and a novel sampling technique to ensure that the generated plans are robust to failures of any single pursuer robot. An implementation and simulation results illustrating the effectiveness of this approach are described.

Rapid Recovery from Robot Failures in Multi-Robot Visibility-Based Pursuit-Evasion

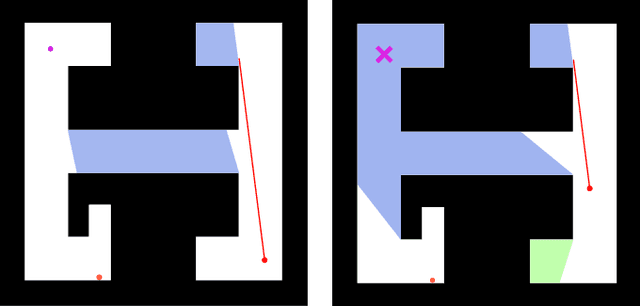
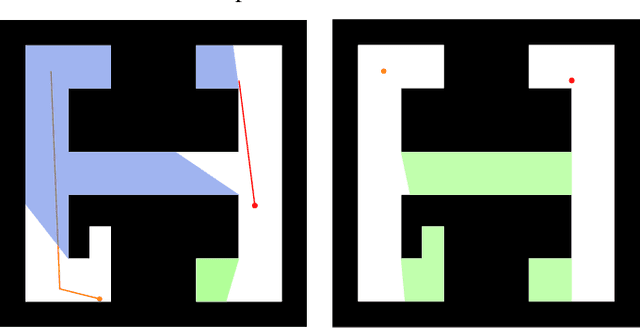
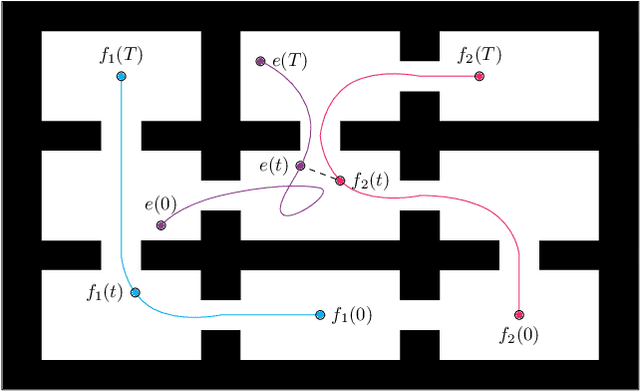
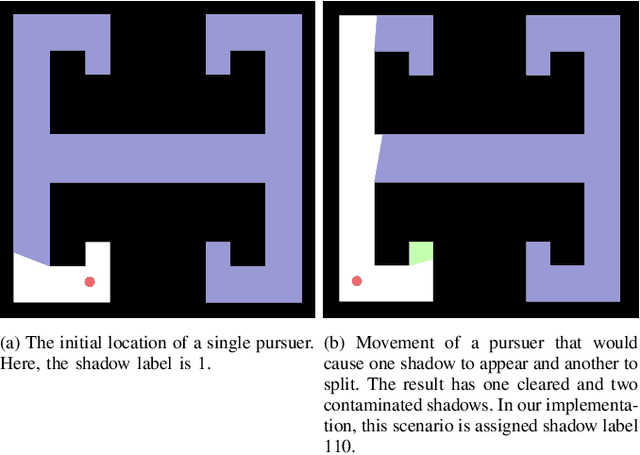
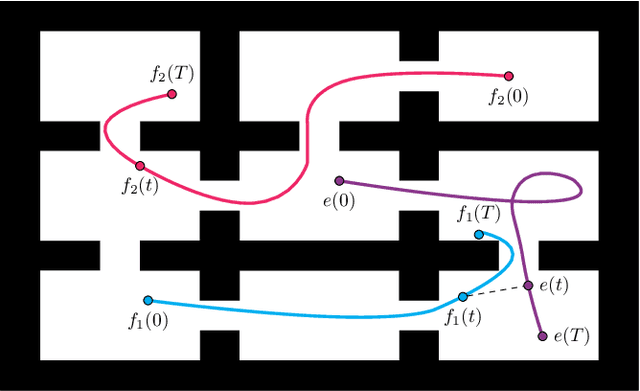
This paper addresses the visibility-based pursuit-evasion problem where a team of pursuer robots operating in a two-dimensional polygonal space seek to establish visibility of an arbitrarily fast evader. This is a computationally challenging task for which the best known complete algorithm takes time doubly exponential in the number of robots. However, recent advances that utilize sampling-based methods have shown progress in generating feasible solutions. An aspect of this problem that has yet to be explored concerns how to ensure that the robots can recover from catastrophic failures which leave one or more robots unexpectedly incapable of continuing to contribute to the pursuit of the evader. To address this issue, we propose an algorithm that can rapidly recover from catastrophic failures. When such failures occur, a replanning occurs, leveraging both the information retained from the previous iteration and the partial progress of the search completed before the failure to generate a new motion strategy for the reduced team of pursuers. We describe an implementation of this algorithm and provide quantitative results that show that the proposed method is able to recover from robot failures more rapidly than a baseline approach that plans from scratch.

A Visibility Roadmap Sampling Approach for a Multi-Robot Visibility-Based Pursuit-Evasion Problem

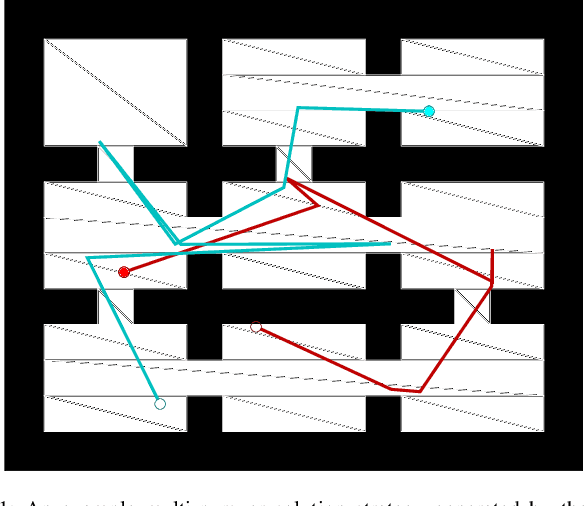
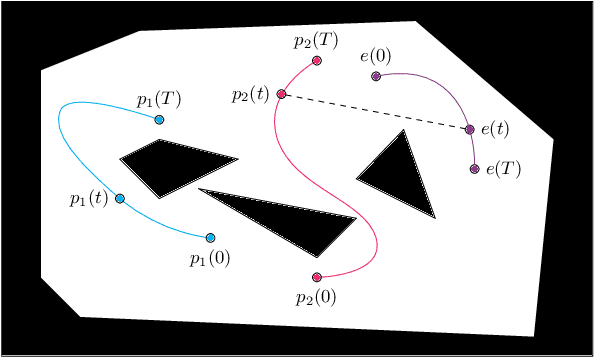
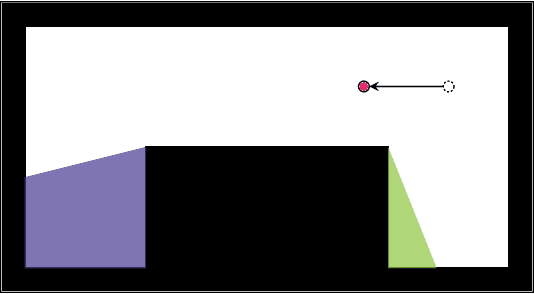
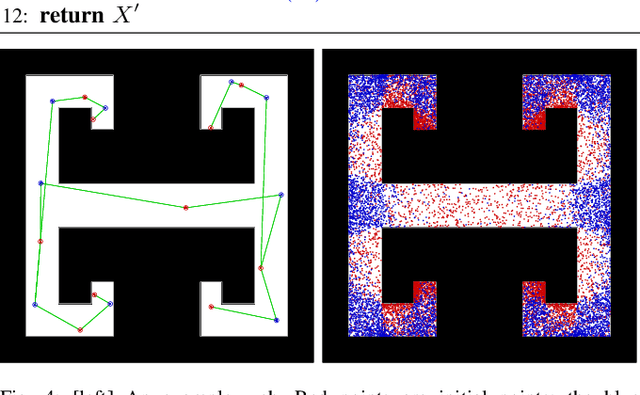
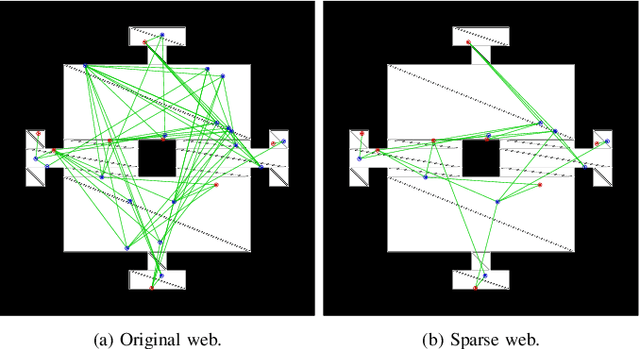
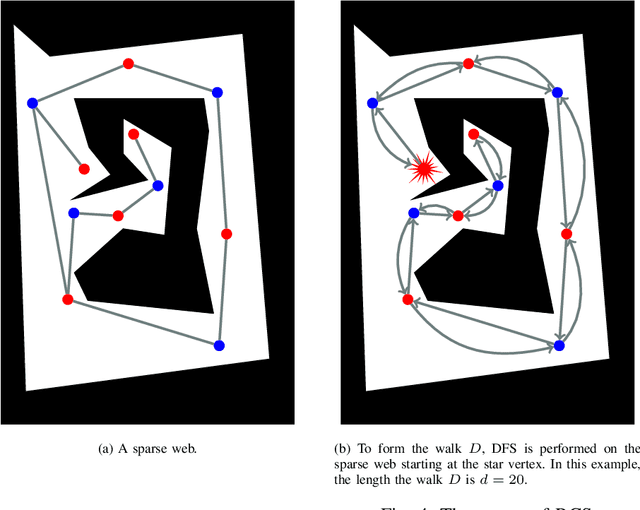
Given a two-dimensional polygonal space, the multi-robot visibility-based pursuit-evasion problem tasks several pursuer robots with the goal of establishing visibility with an arbitrarily fast evader. The best known complete algorithm for this problem takes time doubly exponential in the number of robots. However, sampling-based techniques have shown promise in generating feasible solutions in these scenarios. One of the primary drawbacks to employing existing sampling-based methods is that existing algorithms have long execution times and high failure rates for complex environments. This paper addresses that limitation by proposing a new algorithm that takes an environment as its input and returns a joint motion strategy which ensures that the evader is captured by one of the pursuers. Starting with a single pursuer, we sequentially construct Sample-Generated Pursuit-Evasion Graphs to create such a joint motion strategy. This sequential graph structure ensures that our algorithm will always terminate with a solution, regardless of the complexity of the environment. We describe an implementation of this algorithm and present quantitative results that show significant improvement in comparison to the existing algorithm.

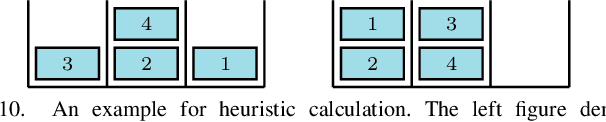
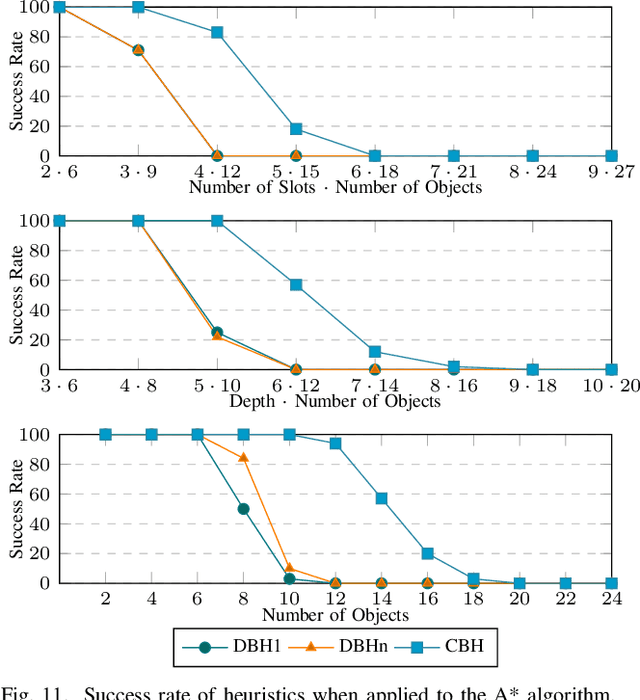
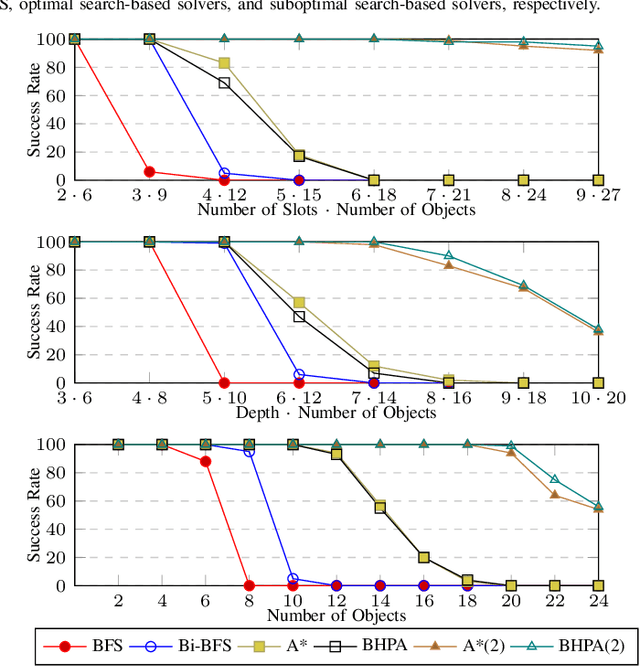
Efficient, High-Quality Stack Rearrangement

This work studies rearrangement problems involving the sorting of robots or objects in stack-like containers, which can be accessed only from one side. Two scenarios are considered: one where every robot or object needs to reach a particular stack, and a setting in which each robot has a distinct position within a stack. In both cases, the goal is to minimize the number of stack removals that need to be performed. Stack rearrangement is shown to be intimately connected to pebble motion problems, a useful abstraction in multi-robot path planning. Through this connection, feasibility of stack rearrangement can be readily addressed. The paper continues to establish lower and upper bounds on optimality, which differ only by a logarithmic factor, in terms of stack removals. An algorithmic solution is then developed that produces suboptimal paths much quicker than a pebble motion solver. Furthermore, informed search-based methods are proposed for finding high-quality solutions. The efficiency and desirable scalability of the methods is demonstrated in simulation.

High-Quality Tabletop Rearrangement with Overhand Grasps: Hardness Results and Fast Methods

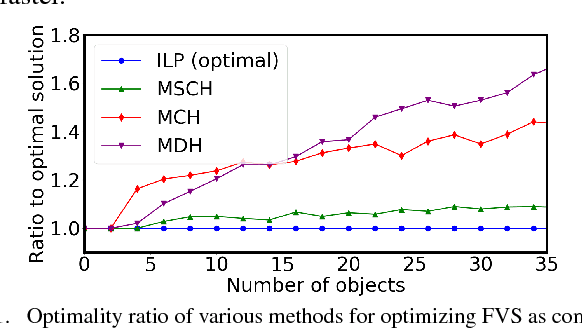
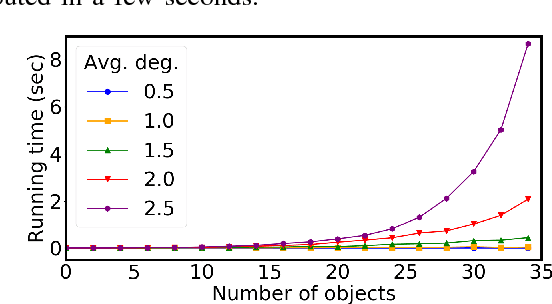
This paper studies the underlying combinatorial structure of a class of object rearrangement problems, which appear frequently in applications. The problems involve multiple, similar-geometry objects placed on a flat, horizontal surface, where a robot can approach them from above and perform pick-and-place operations to rearrange them. The paper considers both the case where the start and goal object poses overlap, and where they do not. For overlapping poses, the primary objective is to minimize the number of pick-and-place actions and then to minimize the distance traveled by the end-effector. For the non-overlapping case, the objective is solely to minimize the end-effector distance. While such problems do not involve all the complexities of general rearrangement, they remain computationally hard challenges in both cases. This is shown through two-way reductions between well-understood, hard combinatorial challenges and these rearrangement problems. The benefit of the reduction is that there are well studied algorithms for solving these well-established combinatorial challenges. These algorithms can be very efficient in practice despite the hardness results. The paper builds on these reduction results to propose an algorithmic pipeline for dealing with the rearrangement problems. Experimental evaluation shows that the proposed pipeline achieves high-quality paths with regards to the optimization objectives. Furthermore, it exhibits highly desirable scalability as the number of objects increases in both the overlapping and non-overlapping setups.