Rapid Recovery from Robot Failures in Multi-Robot Visibility-Based Pursuit-Evasion
Paper and Code
Apr 08, 2021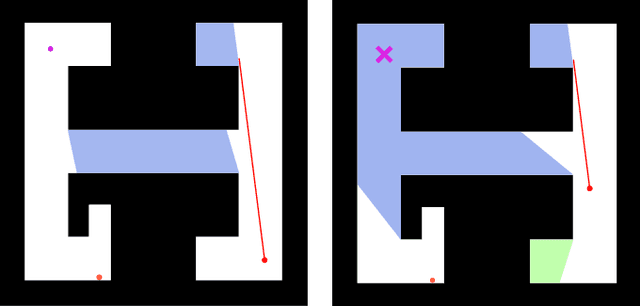
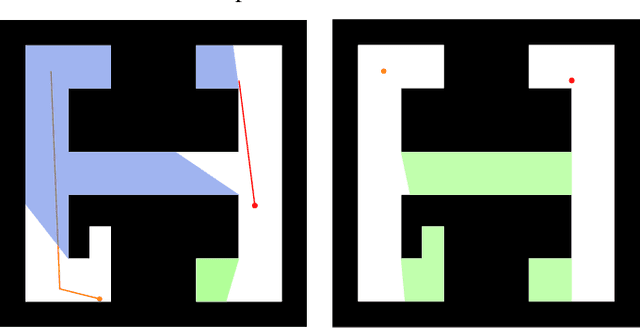
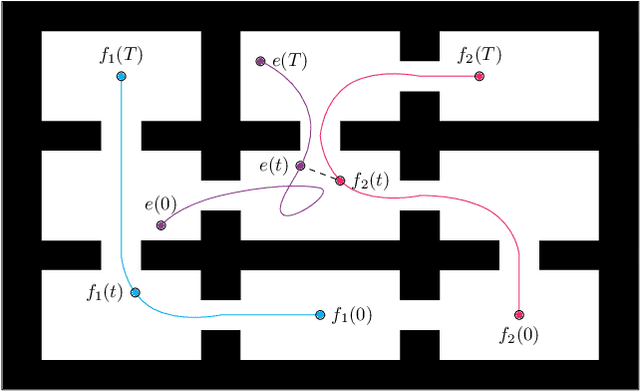
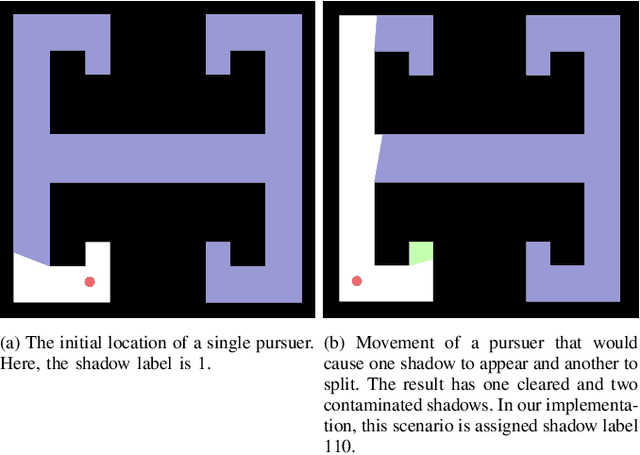
This paper addresses the visibility-based pursuit-evasion problem where a team of pursuer robots operating in a two-dimensional polygonal space seek to establish visibility of an arbitrarily fast evader. This is a computationally challenging task for which the best known complete algorithm takes time doubly exponential in the number of robots. However, recent advances that utilize sampling-based methods have shown progress in generating feasible solutions. An aspect of this problem that has yet to be explored concerns how to ensure that the robots can recover from catastrophic failures which leave one or more robots unexpectedly incapable of continuing to contribute to the pursuit of the evader. To address this issue, we propose an algorithm that can rapidly recover from catastrophic failures. When such failures occur, a replanning occurs, leveraging both the information retained from the previous iteration and the partial progress of the search completed before the failure to generate a new motion strategy for the reduced team of pursuers. We describe an implementation of this algorithm and provide quantitative results that show that the proposed method is able to recover from robot failures more rapidly than a baseline approach that plans from scratch.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge