Efficient, High-Quality Stack Rearrangement
Paper and Code
Jun 29, 2017
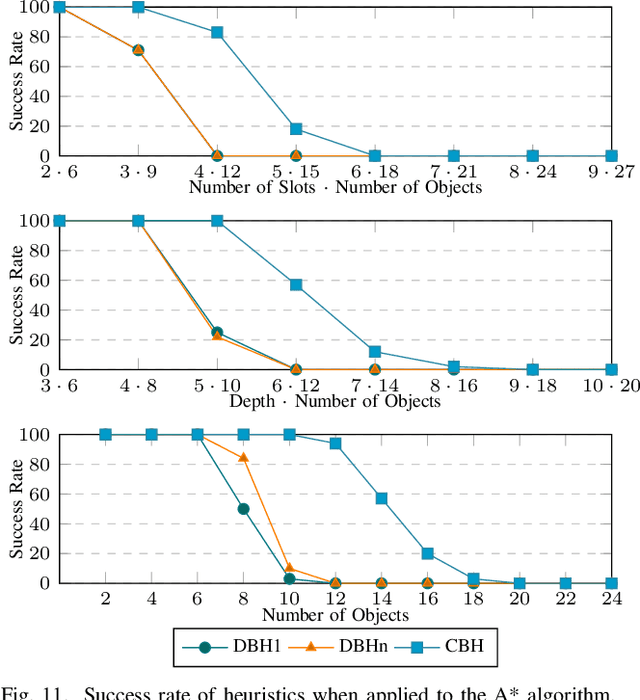
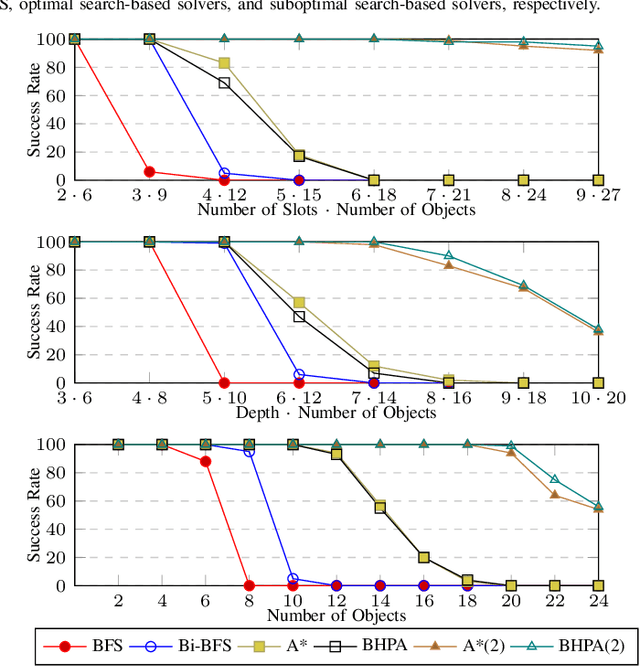
This work studies rearrangement problems involving the sorting of robots or objects in stack-like containers, which can be accessed only from one side. Two scenarios are considered: one where every robot or object needs to reach a particular stack, and a setting in which each robot has a distinct position within a stack. In both cases, the goal is to minimize the number of stack removals that need to be performed. Stack rearrangement is shown to be intimately connected to pebble motion problems, a useful abstraction in multi-robot path planning. Through this connection, feasibility of stack rearrangement can be readily addressed. The paper continues to establish lower and upper bounds on optimality, which differ only by a logarithmic factor, in terms of stack removals. An algorithmic solution is then developed that produces suboptimal paths much quicker than a pebble motion solver. Furthermore, informed search-based methods are proposed for finding high-quality solutions. The efficiency and desirable scalability of the methods is demonstrated in simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge