High-Quality Tabletop Rearrangement with Overhand Grasps: Hardness Results and Fast Methods
Paper and Code
Jun 20, 2017

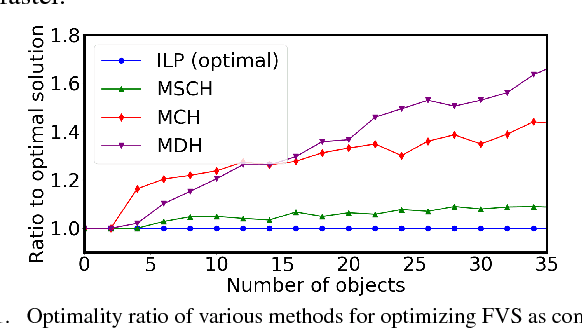
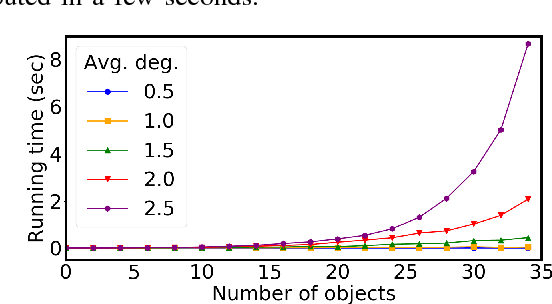
This paper studies the underlying combinatorial structure of a class of object rearrangement problems, which appear frequently in applications. The problems involve multiple, similar-geometry objects placed on a flat, horizontal surface, where a robot can approach them from above and perform pick-and-place operations to rearrange them. The paper considers both the case where the start and goal object poses overlap, and where they do not. For overlapping poses, the primary objective is to minimize the number of pick-and-place actions and then to minimize the distance traveled by the end-effector. For the non-overlapping case, the objective is solely to minimize the end-effector distance. While such problems do not involve all the complexities of general rearrangement, they remain computationally hard challenges in both cases. This is shown through two-way reductions between well-understood, hard combinatorial challenges and these rearrangement problems. The benefit of the reduction is that there are well studied algorithms for solving these well-established combinatorial challenges. These algorithms can be very efficient in practice despite the hardness results. The paper builds on these reduction results to propose an algorithmic pipeline for dealing with the rearrangement problems. Experimental evaluation shows that the proposed pipeline achieves high-quality paths with regards to the optimization objectives. Furthermore, it exhibits highly desirable scalability as the number of objects increases in both the overlapping and non-overlapping setups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge