A Learning and Control Perspective for Microfinance

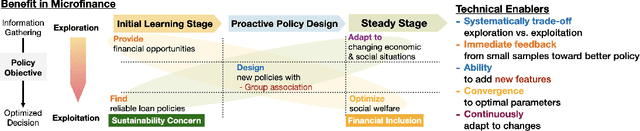
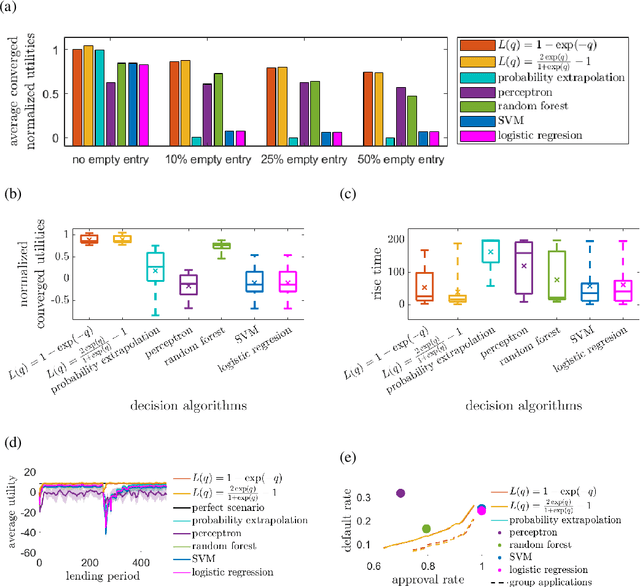
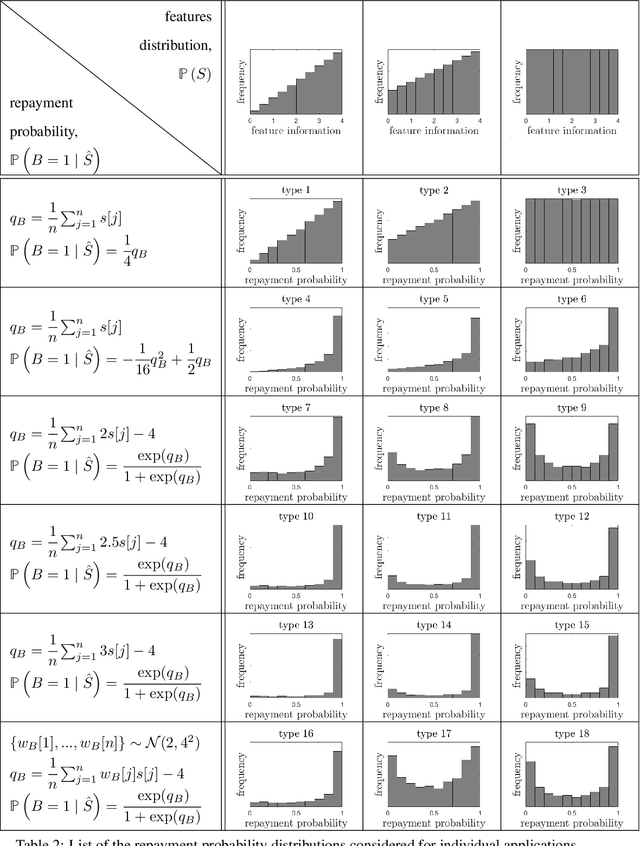
Microfinance in developing areas such as Africa has been proven to improve the local economy significantly. However, many applicants in developing areas cannot provide adequate information required by the financial institution to make a lending decision. As a result, it is challenging for microfinance institutions to assign credit properly based on conventional policies. In this paper, we formulate the decision-making of microfinance into a rigorous optimization-based framework involving learning and control. We propose an algorithm to explore and learn the optimal policy to approve or reject applicants. We provide the conditions under which the algorithms are guaranteed to converge to an optimal one. The proposed algorithm can naturally deal with missing information and systematically tradeoff multiple objectives such as profit maximization, financial inclusion, social benefits, and economic development. Through extensive simulation of both real and synthetic microfinance datasets, we showed our proposed algorithm is superior to existing benchmarks. To the best of our knowledge, this paper is the first to make a connection between microfinance and control and use control-theoretic tools to optimize the policy with a provable guarantee.

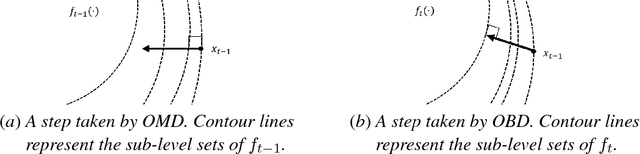
Smoothed Online Convex Optimization in High Dimensions via Online Balanced Descent

We study Smoothed Online Convex Optimization, a version of online convex optimization where the learner incurs a penalty for changing her actions between rounds. Given a $\Omega(\sqrt{d})$ lower bound on the competitive ratio of any online algorithm, where $d$ is the dimension of the action space, we ask under what conditions this bound can be beaten. We introduce a novel algorithmic framework for this problem, Online Balanced Descent (OBD), which works by iteratively projecting the previous point onto a carefully chosen level set of the current cost function so as to balance the switching costs and hitting costs. We demonstrate the generality of the OBD framework by showing how, with different choices of "balance," OBD can improve upon state-of-the-art performance guarantees for both competitive ratio and regret, in particular, OBD is the first algorithm to achieve a dimension-free competitive ratio, $3 + O(1/\alpha)$, for locally polyhedral costs, where $\alpha$ measures the "steepness" of the costs. We also prove bounds on the dynamic regret of OBD when the balance is performed in the dual space that are dimension-free and imply that OBD has sublinear static regret.

Online Convex Optimization Using Predictions

Making use of predictions is a crucial, but under-explored, area of online algorithms. This paper studies a class of online optimization problems where we have external noisy predictions available. We propose a stochastic prediction error model that generalizes prior models in the learning and stochastic control communities, incorporates correlation among prediction errors, and captures the fact that predictions improve as time passes. We prove that achieving sublinear regret and constant competitive ratio for online algorithms requires the use of an unbounded prediction window in adversarial settings, but that under more realistic stochastic prediction error models it is possible to use Averaging Fixed Horizon Control (AFHC) to simultaneously achieve sublinear regret and constant competitive ratio in expectation using only a constant-sized prediction window. Furthermore, we show that the performance of AFHC is tightly concentrated around its mean.