Learning Morphisms with Gauss-Newton Approximation for Growing Networks

A popular method for Neural Architecture Search (NAS) is based on growing networks via small local changes to the network's architecture called network morphisms. These methods start with a small seed network and progressively grow the network by adding new neurons in an automated way. However, it remains a challenge to efficiently determine which parts of the network are best to grow. Here we propose a NAS method for growing a network by using a Gauss-Newton approximation of the loss function to efficiently learn and evaluate candidate network morphisms. We compare our method with state of the art NAS methods for CIFAR-10 and CIFAR-100 classification tasks, and conclude our method learns similar quality or better architectures at a smaller computational cost.

Neural Architecture Search for Parameter-Efficient Fine-tuning of Large Pre-trained Language Models

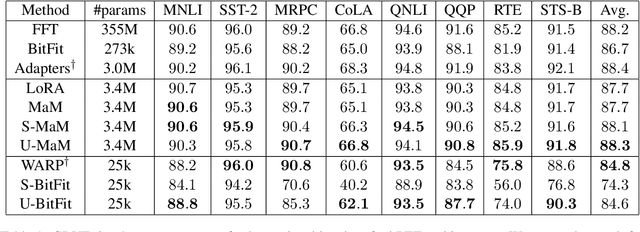
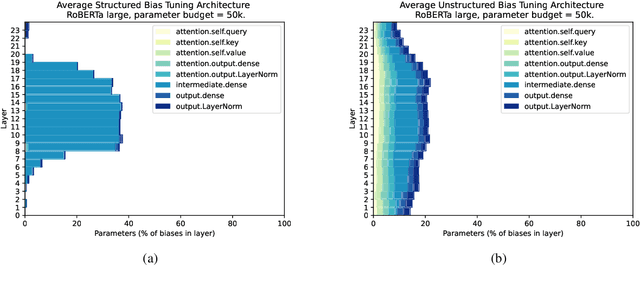
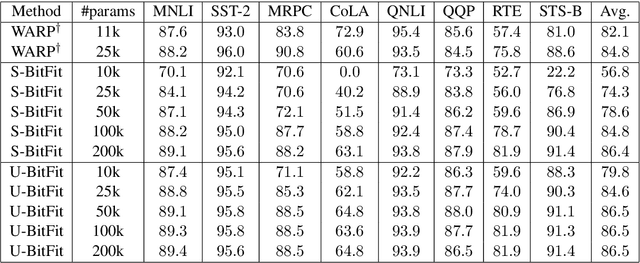
Parameter-efficient tuning (PET) methods fit pre-trained language models (PLMs) to downstream tasks by either computing a small compressed update for a subset of model parameters, or appending and fine-tuning a small number of new model parameters to the pre-trained network. Hand-designed PET architectures from the literature perform well in practice, but have the potential to be improved via automated neural architecture search (NAS). We propose an efficient NAS method for learning PET architectures via structured and unstructured pruning. We present experiments on GLUE demonstrating the effectiveness of our algorithm and discuss how PET architectural design choices affect performance in practice.

A Forest Mixture Bound for Block-Free Parallel Inference

Coordinate ascent variational inference is an important algorithm for inference in probabilistic models, but it is slow because it updates only a single variable at a time. Block coordinate methods perform inference faster by updating blocks of variables in parallel. However, the speed and stability of these algorithms depends on how the variables are partitioned into blocks. In this paper, we give a stable parallel algorithm for inference in deep exponential families that doesn't require the variables to be partitioned into blocks. We achieve this by lower bounding the ELBO by a new objective we call the forest mixture bound (FM bound) that separates the inference problem for variables within a hidden layer. We apply this to the simple case when all random variables are Gaussian and show empirically that the algorithm converges faster for models that are inherently more forest-like.