Latent Mode Decomposition

We introduce Variational Latent Mode Decomposition (VLMD), a new algorithm for extracting oscillatory modes and associated connectivity structures from multivariate signals. VLMD addresses key limitations of existing Multivariate Mode Decomposition (MMD) techniques -including high computational cost, sensitivity to parameter choices, and weak modeling of interchannel dependencies. Its improved performance is driven by a novel underlying model, Latent Mode Decomposition (LMD), which blends sparse coding and mode decomposition to represent multichannel signals as sparse linear combinations of shared latent components composed of AM-FM oscillatory modes. This formulation enables VLMD to operate in a lower-dimensional latent space, enhancing robustness to noise, scalability, and interpretability. The algorithm solves a constrained variational optimization problem that jointly enforces reconstruction fidelity, sparsity, and frequency regularization. Experiments on synthetic and real-world datasets demonstrate that VLMD outperforms state-of-the-art MMD methods in accuracy, efficiency, and interpretability of extracted structures.

Successive Jump and Mode Decomposition

We propose fully data-driven variational methods, termed successive jump and mode decomposition (SJMD) and its multivariate extension, successive multivariate jump and mode decomposition (SMJMD), for successively decomposing nonstationary signals into amplitude- and frequency-modulated (AM-FM) oscillations and jump components. Unlike existing methods that treat oscillatory modes and jump discontinuities separately and often require prior knowledge of the number of components (K) -- which is difficult to obtain in practice -- our approaches employ successive optimization-based schemes that jointly handle AM-FM oscillations and jump discontinuities without the need to predefine K. Empirical evaluations on synthetic and real-world datasets demonstrate that the proposed algorithms offer superior accuracy and computational efficiency compared to state-of-the-art methods.

Jump Plus AM-FM Mode Decomposition

A novel method for decomposing a nonstationary signal into amplitude- and frequency-modulated (AM-FM) oscillations and discontinuous (jump) components is proposed. Current nonstationary signal decomposition methods are designed to either obtain constituent AM-FM oscillatory modes or the discontinuous and residual components from the data, separately. Yet, many real-world signals of interest simultaneously exhibit both behaviors i.e., jumps and oscillations. Currently, no available method can extract jumps and AM-FM oscillatory components directly from the data. In our novel approach, we design and solve a variational optimization problem to accomplish this task. The optimization formulation includes a regularization term to minimize the bandwidth of all signal modes for effective oscillation modeling, and a prior for extracting the jump component. Our method addresses the limitations of conventional AM-FM signal decomposition methods in extracting jumps, as well as the limitations of existing jump extraction methods in decomposing multiscale oscillations. By employing an optimization framework that accounts for both multiscale oscillatory components and discontinuities, our methods show superior performance compared to existing decomposition techniques. We demonstrate the effectiveness of our approaches on synthetic, real-world, single-channel, and multivariate data, highlighting their utility in three specific applications: Earth's electric field signals, electrocardiograms (ECG), and electroencephalograms (EEG).

Time-Varying Graph Mode Decomposition

Time-varying graph signals are alternative representation of multivariate (or multichannel) signals in which a single time-series is associated with each of the nodes or vertex of a graph. Aided by the graph-theoretic tools, time-varying graph models have the ability to capture the underlying structure of the data associated with multiple nodes of a graph -- a feat that is hard to accomplish using standard signal processing approaches. The aim of this contribution is to propose a method for the decomposition of time-varying graph signals into a set of graph modes. The graph modes can be interpreted in terms of their temporal, spectral and topological characteristics. From the temporal (spectral) viewpoint, the graph modes represent the finite number of oscillatory signal components (output of multiple band-pass filters whose center frequencies and bandwidths are learned in a fully data-driven manner), similar in properties to those obtained from the empirical mode decomposition and related approaches. From the topological perspective, the graph modes quantify the functional connectivity of the graph vertices at multiple scales based on their signal content. In order to estimate the graph modes, a variational optimization formulation is designed that includes necessary temporal, spectral and topological requirements relevant to the graph modes. An efficient method to solve that problem is developed which is based on the alternating direction method of multipliers (ADMM) and the primal-dual optimization approach. Finally, the ability of the method to enable a joint analysis of the temporal and topological characteristics of time-varying graph signals, at multiple frequency bands/scales, is demonstrated on a series of synthetic and real time-varying graph data sets.

Data-driven Signal Decomposition Approaches: A Comparative Analysis

Signal decomposition (SD) approaches aim to decompose non-stationary signals into their constituent amplitude- and frequency-modulated components. This represents an important preprocessing step in many practical signal processing pipelines, providing useful knowledge and insight into the data and relevant underlying system(s) while also facilitating tasks such as noise or artefact removal and feature extraction. The popular SD methods are mostly data-driven, striving to obtain inherent well-behaved signal components without making many prior assumptions on input data. Among those methods include empirical mode decomposition (EMD) and variants, variational mode decomposition (VMD) and variants, synchrosqueezed transform (SST) and variants and sliding singular spectrum analysis (SSA). With the increasing popularity and utility of these methods in wide-ranging application, it is imperative to gain a better understanding and insight into the operation of these algorithms, evaluate their accuracy with and without noise in input data and gauge their sensitivity against algorithmic parameter changes. In this work, we achieve those tasks through extensive experiments involving carefully designed synthetic and real-life signals. Based on our experimental observations, we comment on the pros and cons of the considered SD algorithms as well as highlighting the best practices, in terms of parameter selection, for the their successful operation. The SD algorithms for both single- and multi-channel (multivariate) data fall within the scope of our work. For multivariate signals, we evaluate the performance of the popular algorithms in terms of fulfilling the mode-alignment property, especially in the presence of noise.

A Generic Framework for Assessing the Performance Bounds of Image Feature Detectors

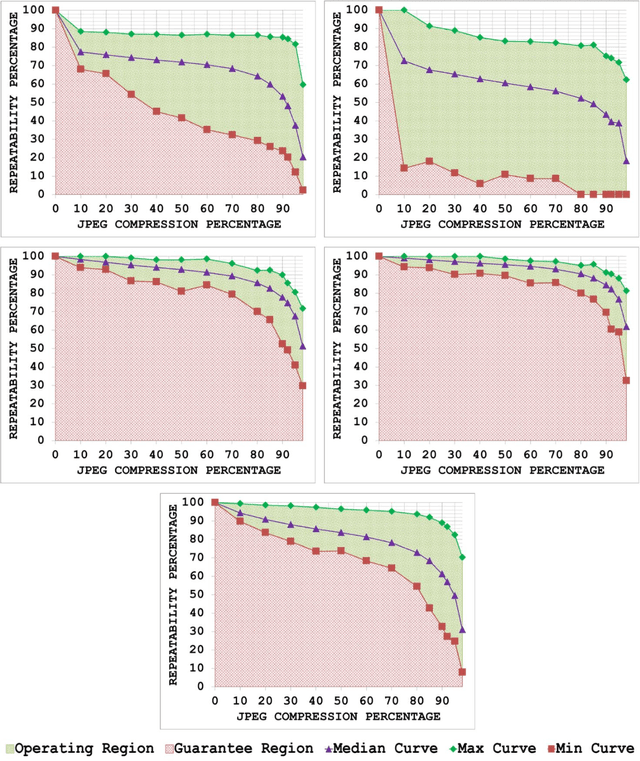
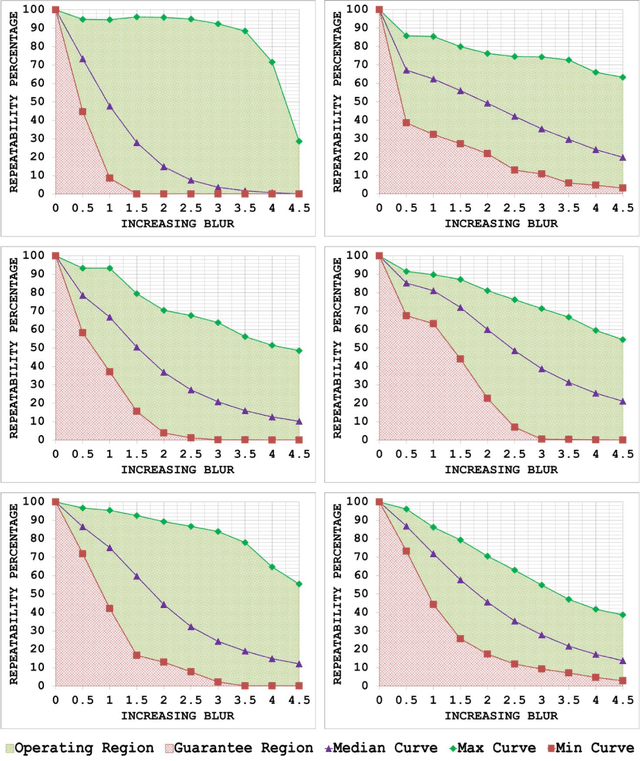
Since local feature detection has been one of the most active research areas in computer vision during the last decade, a large number of detectors have been proposed. The interest in feature-based applications continues to grow and has thus rendered the task of characterizing the performance of various feature detection methods an important issue in vision research. Inspired by the good practices of electronic system design, a generic framework based on the repeatability measure is presented in this paper that allows assessment of the upper and lower bounds of detector performance and finds statistically significant performance differences between detectors as a function of image transformation amount by introducing a new variant of McNemars test in an effort to design more reliable and effective vision systems. The proposed framework is then employed to establish operating and guarantee regions for several state-of-the-art detectors and to identify their statistical performance differences for three specific image transformations: JPEG compression, uniform light changes and blurring. The results are obtained using a newly acquired, large image database (20482) images with 539 different scenes. These results provide new insights into the behaviour of detectors and are also useful from the vision systems design perspective.

Integral Images: Efficient Algorithms for Their Computation and Storage in Resource-Constrained Embedded Vision Systems

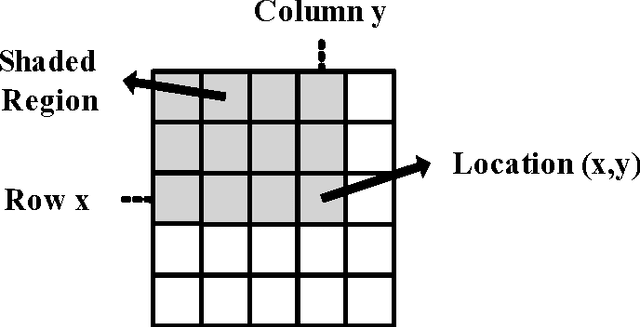
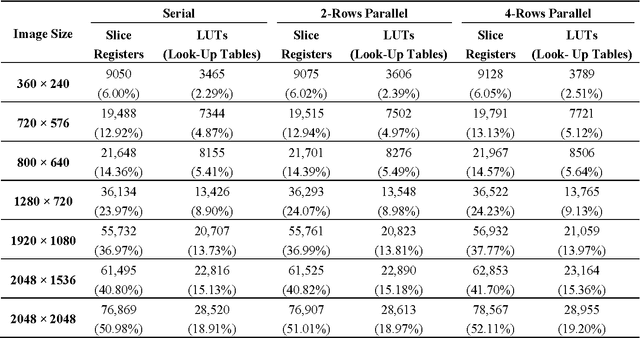
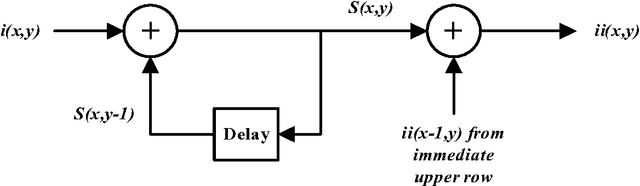
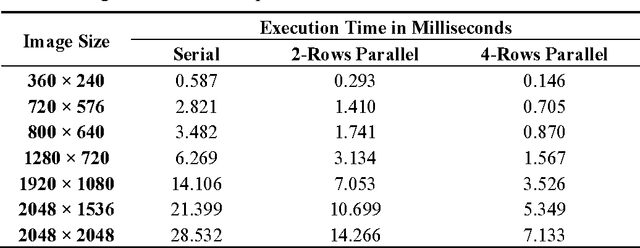
The integral image, an intermediate image representation, has found extensive use in multi-scale local feature detection algorithms, such as Speeded-Up Robust Features (SURF), allowing fast computation of rectangular features at constant speed, independent of filter size. For resource-constrained real-time embedded vision systems, computation and storage of integral image presents several design challenges due to strict timing and hardware limitations. Although calculation of the integral image only consists of simple addition operations, the total number of operations is large owing to the generally large size of image data. Recursive equations allow substantial decrease in the number of operations but require calculation in a serial fashion. This paper presents two new hardware algorithms that are based on the decomposition of these recursive equations, allowing calculation of up to four integral image values in a row-parallel way without significantly increasing the number of operations. An efficient design strategy is also proposed for a parallel integral image computation unit to reduce the size of the required internal memory (nearly 35% for common HD video). Addressing the storage problem of integral image in embedded vision systems, the paper presents two algorithms which allow substantial decrease (at least 44.44%) in the memory requirements. Finally, the paper provides a case study that highlights the utility of the proposed architectures in embedded vision systems.