Quantum Compressive Sensing: Mathematical Machinery, Quantum Algorithms, and Quantum Circuitry

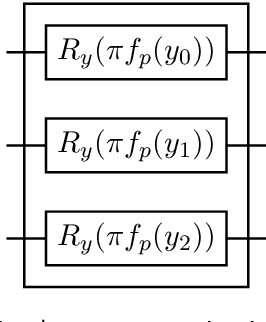
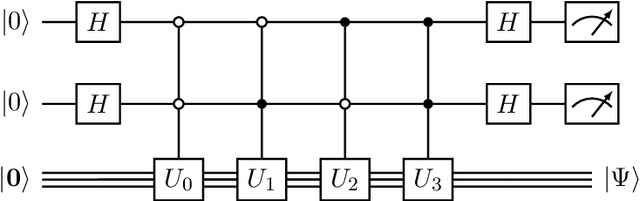
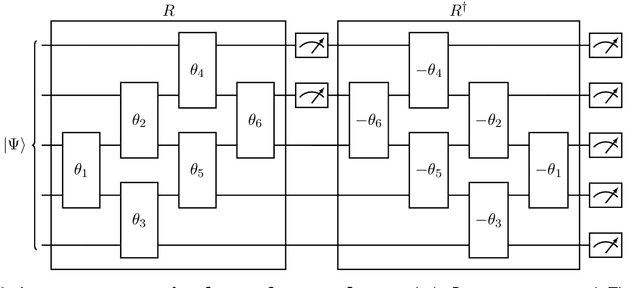
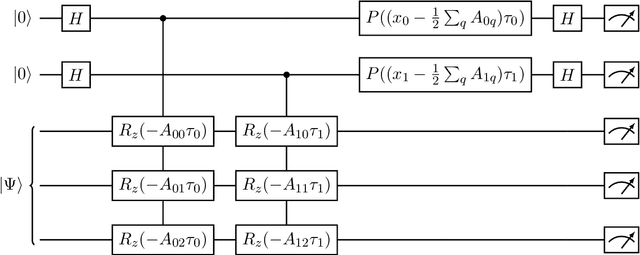
Compressive sensing is a sensing protocol that facilitates reconstruction of large signals from relatively few measurements by exploiting known structures of signals of interest, typically manifested as signal sparsity. Compressive sensing's vast repertoire of applications in areas such as communications and image reconstruction stems from the traditional approach of utilizing non-linear optimization to exploit the sparsity assumption by selecting the lowest-weight (i.e. maximum sparsity) signal consistent with all acquired measurements. Recent efforts in the literature consider instead a data-driven approach, training tensor networks to learn the structure of signals of interest. The trained tensor network is updated to "project" its state onto one consistent with the measurements taken, and is then sampled site by site to "guess" the original signal. In this paper, we take advantage of this computing protocol by formulating an alternative "quantum" protocol, in which the state of the tensor network is a quantum state over a set of entangled qubits. Accordingly, we present the associated algorithms and quantum circuits required to implement the training, projection, and sampling steps on a quantum computer. We supplement our theoretical results by simulating the proposed circuits with a small, qualitative model of LIDAR imaging of earth forests. Our results indicate that a quantum, data-driven approach to compressive sensing, may have significant promise as quantum technology continues to make new leaps.

Unfolded Algorithms for Deep Phase Retrieval

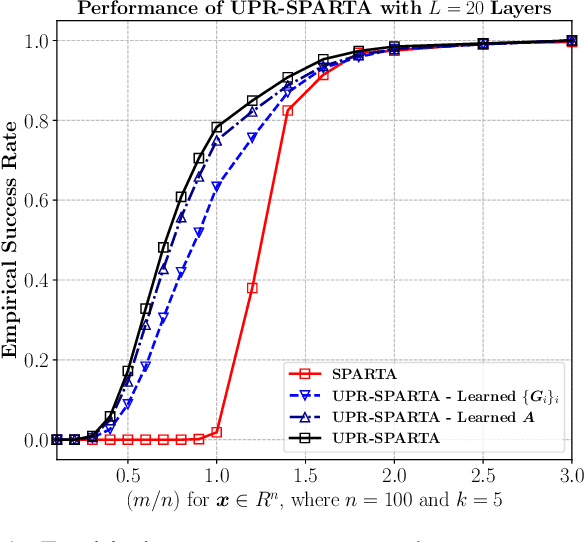
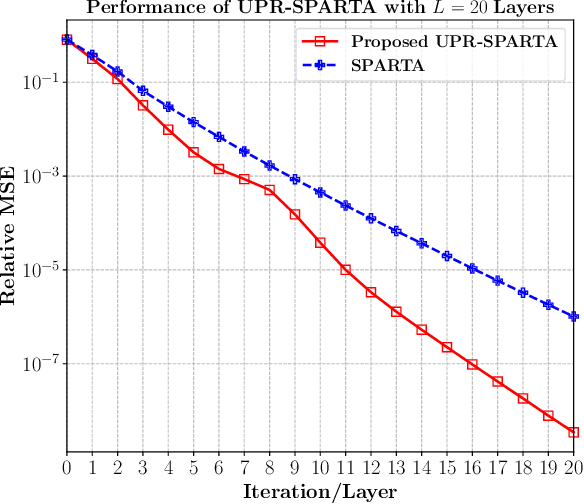
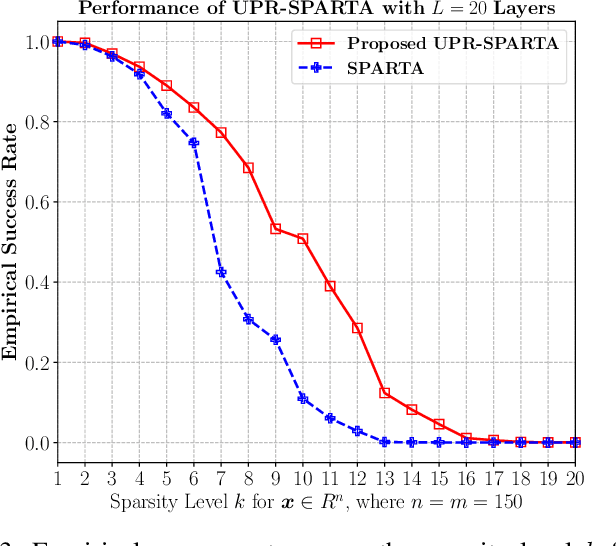
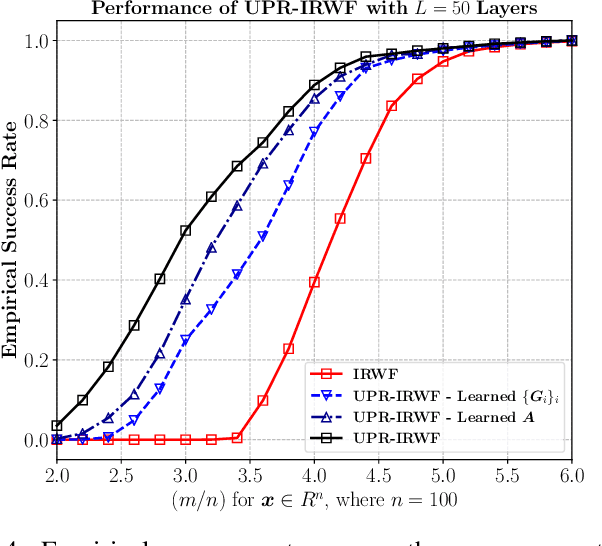
Exploring the idea of phase retrieval has been intriguing researchers for decades, due to its appearance in a wide range of applications. The task of a phase retrieval algorithm is typically to recover a signal from linear phaseless measurements. In this paper, we approach the problem by proposing a hybrid model-based data-driven deep architecture, referred to as Unfolded Phase Retrieval (UPR), that exhibits significant potential in improving the performance of state-of-the art data-driven and model-based phase retrieval algorithms. The proposed method benefits from versatility and interpretability of well-established model-based algorithms, while simultaneously benefiting from the expressive power of deep neural networks. In particular, our proposed model-based deep architecture is applied to the conventional phase retrieval problem (via the incremental reshaped Wirtinger flow algorithm) and the sparse phase retrieval problem (via the sparse truncated amplitude flow algorithm), showing immense promise in both cases. Furthermore, we consider a joint design of the sensing matrix and the signal processing algorithm and utilize the deep unfolding technique in the process. Our numerical results illustrate the effectiveness of such hybrid model-based and data-driven frameworks and showcase the untapped potential of data-aided methodologies to enhance the existing phase retrieval algorithms.

UPR: A Model-Driven Architecture for Deep Phase Retrieval

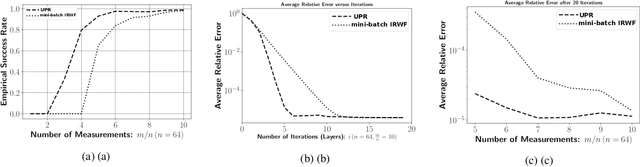
The problem of phase retrieval has been intriguing researchers for decades due to its appearance in a wide range of applications. The task of a phase retrieval algorithm is typically to recover a signal from linear phase-less measurements. In this paper, we approach the problem by proposing a hybrid model-based data-driven deep architecture, referred to as the Unfolded Phase Retrieval (UPR), that shows potential in improving the performance of the state-of-the-art phase retrieval algorithms. Specifically, the proposed method benefits from versatility and interpretability of well established model-based algorithms, while simultaneously benefiting from the expressive power of deep neural networks. Our numerical results illustrate the effectiveness of such hybrid deep architectures and showcase the untapped potential of data-aided methodologies to enhance the existing phase retrieval algorithms.

Deep Signal Recovery with One-Bit Quantization

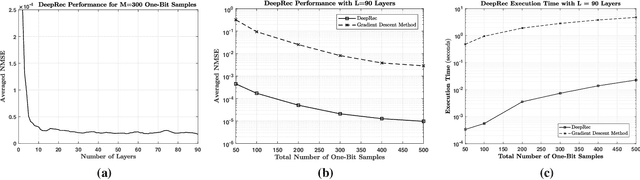
Machine learning, and more specifically deep learning, have shown remarkable performance in sensing, communications, and inference. In this paper, we consider the application of the deep unfolding technique in the problem of signal reconstruction from its one-bit noisy measurements. Namely, we propose a model-based machine learning method and unfold the iterations of an inference optimization algorithm into the layers of a deep neural network for one-bit signal recovery. The resulting network, which we refer to as DeepRec, can efficiently handle the recovery of high-dimensional signals from acquired one-bit noisy measurements. The proposed method results in an improvement in accuracy and computational efficiency with respect to the original framework as shown through numerical analysis.