Quantum Compressive Sensing: Mathematical Machinery, Quantum Algorithms, and Quantum Circuitry
Paper and Code
Apr 27, 2022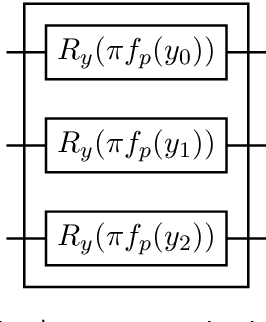
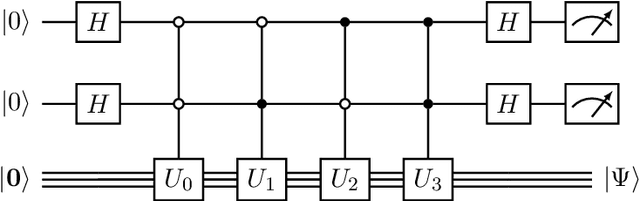
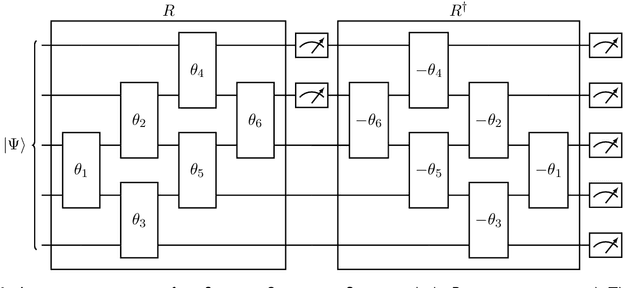
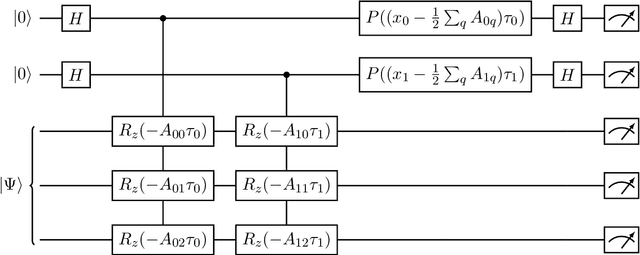
Compressive sensing is a sensing protocol that facilitates reconstruction of large signals from relatively few measurements by exploiting known structures of signals of interest, typically manifested as signal sparsity. Compressive sensing's vast repertoire of applications in areas such as communications and image reconstruction stems from the traditional approach of utilizing non-linear optimization to exploit the sparsity assumption by selecting the lowest-weight (i.e. maximum sparsity) signal consistent with all acquired measurements. Recent efforts in the literature consider instead a data-driven approach, training tensor networks to learn the structure of signals of interest. The trained tensor network is updated to "project" its state onto one consistent with the measurements taken, and is then sampled site by site to "guess" the original signal. In this paper, we take advantage of this computing protocol by formulating an alternative "quantum" protocol, in which the state of the tensor network is a quantum state over a set of entangled qubits. Accordingly, we present the associated algorithms and quantum circuits required to implement the training, projection, and sampling steps on a quantum computer. We supplement our theoretical results by simulating the proposed circuits with a small, qualitative model of LIDAR imaging of earth forests. Our results indicate that a quantum, data-driven approach to compressive sensing, may have significant promise as quantum technology continues to make new leaps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge