When Witnesses Defend: A Witness Graph Topological Layer for Adversarial Graph Learning

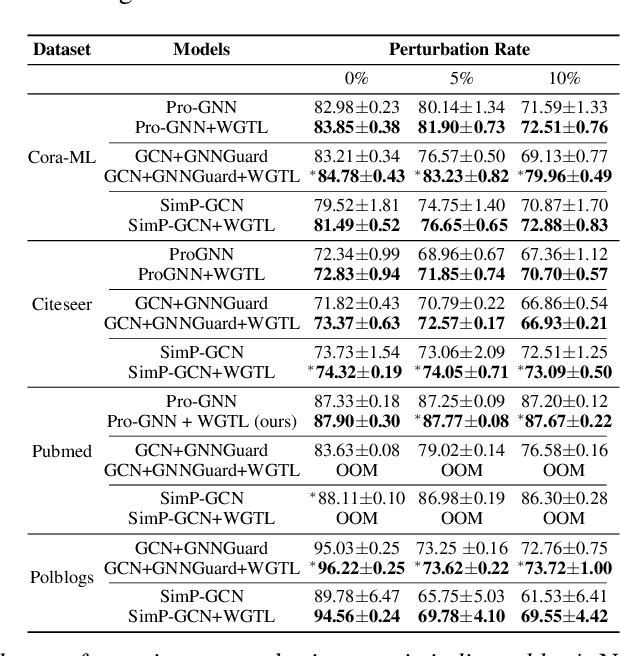
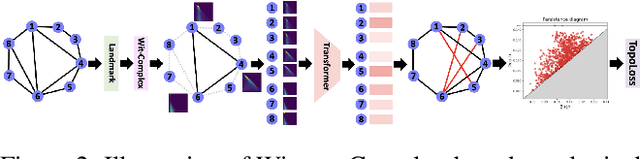
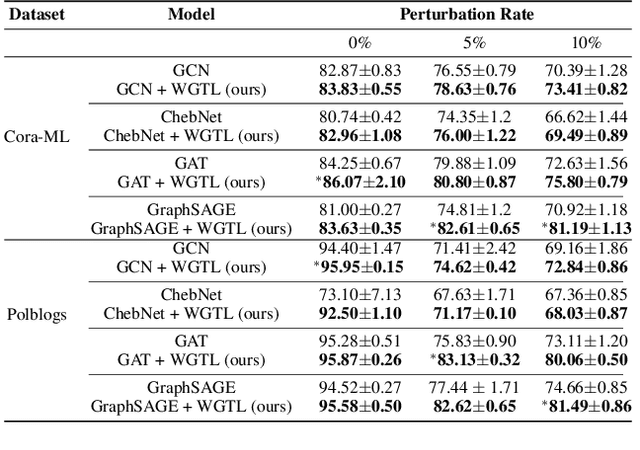
Capitalizing on the intuitive premise that shape characteristics are more robust to perturbations, we bridge adversarial graph learning with the emerging tools from computational topology, namely, persistent homology representations of graphs. We introduce the concept of witness complex to adversarial analysis on graphs, which allows us to focus only on the salient shape characteristics of graphs, yielded by the subset of the most essential nodes (i.e., landmarks), with minimal loss of topological information on the whole graph. The remaining nodes are then used as witnesses, governing which higher-order graph substructures are incorporated into the learning process. Armed with the witness mechanism, we design Witness Graph Topological Layer (WGTL), which systematically integrates both local and global topological graph feature representations, the impact of which is, in turn, automatically controlled by the robust regularized topological loss. Given the attacker's budget, we derive the important stability guarantees of both local and global topology encodings and the associated robust topological loss. We illustrate the versatility and efficiency of WGTL by its integration with five GNNs and three existing non-topological defense mechanisms. Our extensive experiments across six datasets demonstrate that WGTL boosts the robustness of GNNs across a range of perturbations and against a range of adversarial attacks, leading to relative gains of up to 18%.

Finite Volume Features, Global Geometry Representations, and Residual Training for Deep Learning-based CFD Simulation

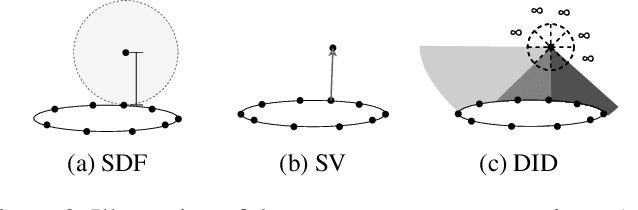
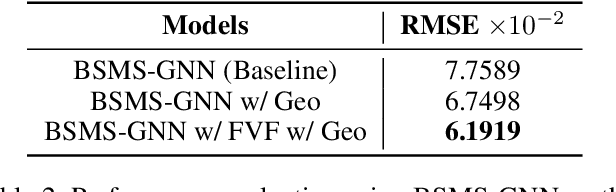
Computational fluid dynamics (CFD) simulation is an irreplaceable modelling step in many engineering designs, but it is often computationally expensive. Some graph neural network (GNN)-based CFD methods have been proposed. However, the current methods inherit the weakness of traditional numerical simulators, as well as ignore the cell characteristics in the mesh used in the finite volume method, a common method in practical CFD applications. Specifically, the input nodes in these GNN methods have very limited information about any object immersed in the simulation domain and its surrounding environment. Also, the cell characteristics of the mesh such as cell volume, face surface area, and face centroid are not included in the message-passing operations in the GNN methods. To address these weaknesses, this work proposes two novel geometric representations: Shortest Vector (SV) and Directional Integrated Distance (DID). Extracted from the mesh, the SV and DID provide global geometry perspective to each input node, thus removing the need to collect this information through message-passing. This work also introduces the use of Finite Volume Features (FVF) in the graph convolutions as node and edge attributes, enabling its message-passing operations to adjust to different nodes. Finally, this work is the first to demonstrate how residual training, with the availability of low-resolution data, can be adopted to improve the flow field prediction accuracy. Experimental results on two datasets with five different state-of-the-art GNN methods for CFD indicate that SV, DID, FVF and residual training can effectively reduce the predictive error of current GNN-based methods by as much as 41%.