Compiling to recurrent neurons

Discrete structures are currently second-class in differentiable programming. Since functions over discrete structures lack overt derivatives, differentiable programs do not differentiate through them and limit where they can be used. For example, when programming a neural network, conditionals and iteration cannot be used everywhere; they can break the derivatives necessary for gradient-based learning to work. This limits the class of differentiable algorithms we can directly express, imposing restraints on how we build neural networks and differentiable programs more generally. However, these restraints are not fundamental. Recent work shows conditionals can be first-class, by compiling them into differentiable form as linear neurons. Similarly, this work shows iteration can be first-class -- by compiling to linear recurrent neurons. We present a minimal typed, higher-order and linear programming language with iteration called $\textsf{Cajal}\scriptstyle(\mathbb{\multimap}, \mathbb{2}, \mathbb{N})$. We prove its programs compile correctly to recurrent neurons, allowing discrete algorithms to be expressed in a differentiable form compatible with gradient-based learning. With our implementation, we conduct two experiments where we link these recurrent neurons against a neural network solving an iterative image transformation task. This determines part of its function prior to learning. As a result, the network learns faster and with greater data-efficiency relative to a neural network programmed without first-class iteration. A key lesson is that recurrent neurons enable a rich interplay between learning and the discrete structures of ordinary programming.

Compiling to linear neurons

We don't program neural networks directly. Instead, we rely on an indirect style where learning algorithms, like gradient descent, determine a neural network's function by learning from data. This indirect style is often a virtue; it empowers us to solve problems that were previously impossible. But it lacks discrete structure. We can't compile most algorithms into a neural network -- even if these algorithms could help the network learn. This limitation occurs because discrete algorithms are not obviously differentiable, making them incompatible with the gradient-based learning algorithms that determine a neural network's function. To address this, we introduce $\textsf{Cajal}$: a typed, higher-order and linear programming language intended to be a minimal vehicle for exploring a direct style of programming neural networks. We prove $\textsf{Cajal}$ programs compile to linear neurons, allowing discrete algorithms to be expressed in a differentiable form compatible with gradient-based learning. With our implementation of $\textsf{Cajal}$, we conduct several experiments where we link these linear neurons against other neural networks to determine part of their function prior to learning. Linking with these neurons allows networks to learn faster, with greater data-efficiency, and in a way that's easier to debug. A key lesson is that linear programming languages provide a path towards directly programming neural networks, enabling a rich interplay between learning and the discrete structures of ordinary programming.

DafnyBench: A Benchmark for Formal Software Verification

We introduce DafnyBench, the largest benchmark of its kind for training and evaluating machine learning systems for formal software verification. We test the ability of LLMs such as GPT-4 and Claude 3 to auto-generate enough hints for the Dafny formal verification engine to successfully verify over 750 programs with about 53,000 lines of code. The best model and prompting scheme achieved 68% success rate, and we quantify how this rate improves when retrying with error message feedback and how it deteriorates with the amount of required code and hints. We hope that DafnyBench will enable rapid improvements from this baseline as LLMs and verification techniques grow in quality.

Verified Multi-Step Synthesis using Large Language Models and Monte Carlo Tree Search

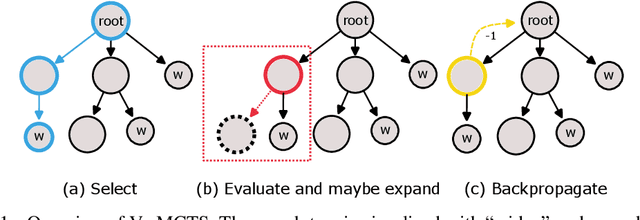
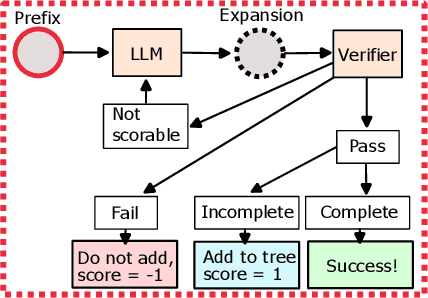
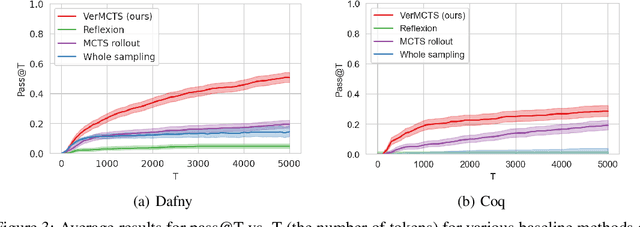
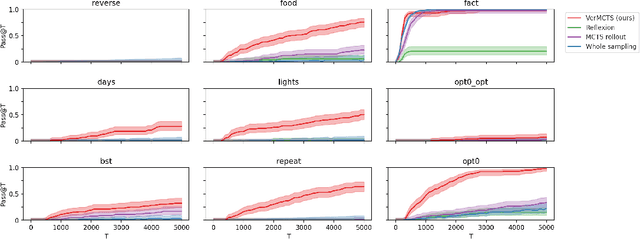
We present an approach using Monte Carlo Tree Search (MCTS) to guide Large Language Models (LLMs) to generate verified programs in Dafny, Lean and Coq. Our method, which we call VMCTS, leverages the verifier inside the search algorithm by checking partial programs at each step. In combination with the LLM prior, the verifier feedback raises the synthesis capabilities of open source models. On a set of five verified programming problems, we find that in four problems where the base model cannot solve the question even when re-sampling solutions for one hour, VMCTS can solve the problems within 6 minutes. The base model with VMCTS is even competitive with ChatGPT4 augmented with plugins and multiple re-tries on these problems. Our code and benchmarks are available at https://github.com/namin/llm-verified-with-monte-carlo-tree-search .