Online Backfilling with No Regret for Large-Scale Image Retrieval

Backfilling is the process of re-extracting all gallery embeddings from upgraded models in image retrieval systems. It inevitably requires a prohibitively large amount of computational cost and even entails the downtime of the service. Although backward-compatible learning sidesteps this challenge by tackling query-side representations, this leads to suboptimal solutions in principle because gallery embeddings cannot benefit from model upgrades. We address this dilemma by introducing an online backfilling algorithm, which enables us to achieve a progressive performance improvement during the backfilling process while not sacrificing the final performance of new model after the completion of backfilling. To this end, we first propose a simple distance rank merge technique for online backfilling. Then, we incorporate a reverse transformation module for more effective and efficient merging, which is further enhanced by adopting a metric-compatible contrastive learning approach. These two components help to make the distances of old and new models compatible, resulting in desirable merge results during backfilling with no extra computational overhead. Extensive experiments show the effectiveness of our framework on four standard benchmarks in various settings.

A Reinforcement Learning Approach to the View Planning Problem

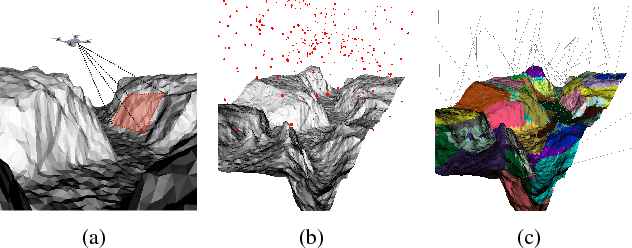
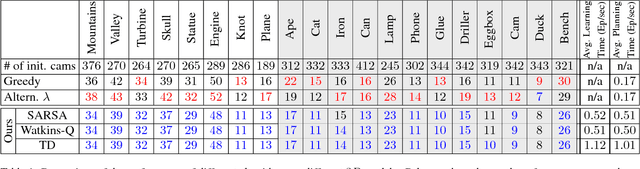
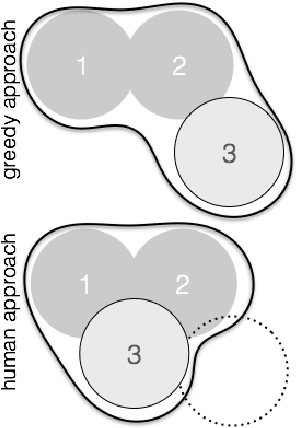
We present a Reinforcement Learning (RL) solution to the view planning problem (VPP), which generates a sequence of view points that are capable of sensing all accessible area of a given object represented as a 3D model. In doing so, the goal is to minimize the number of view points, making the VPP a class of set covering optimization problem (SCOP). The SCOP is NP-hard, and the inapproximability results tell us that the greedy algorithm provides the best approximation that runs in polynomial time. In order to find a solution that is better than the greedy algorithm, (i) we introduce a novel score function by exploiting the geometry of the 3D model, (ii) we model an intuitive human approach to VPP using this score function, and (iii) we cast VPP as a Markovian Decision Process (MDP), and solve the MDP in RL framework using well-known RL algorithms. In particular, we use SARSA, Watkins-Q and TD with function approximation to solve the MDP. We compare the results of our method with the baseline greedy algorithm in an extensive set of test objects, and show that we can out-perform the baseline in almost all cases.