Fast Estimation of Partial Dependence Functions using Trees

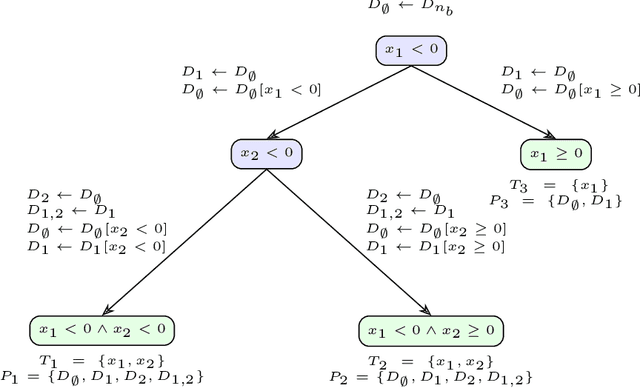
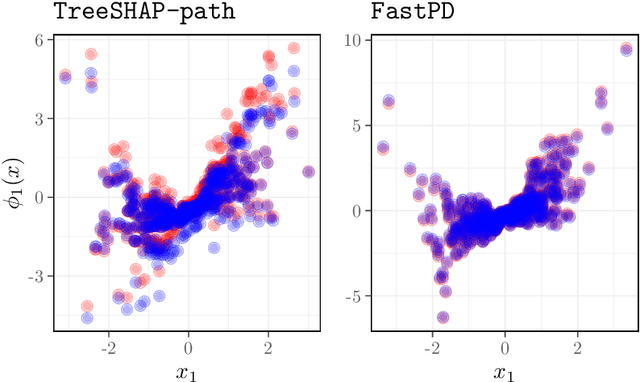
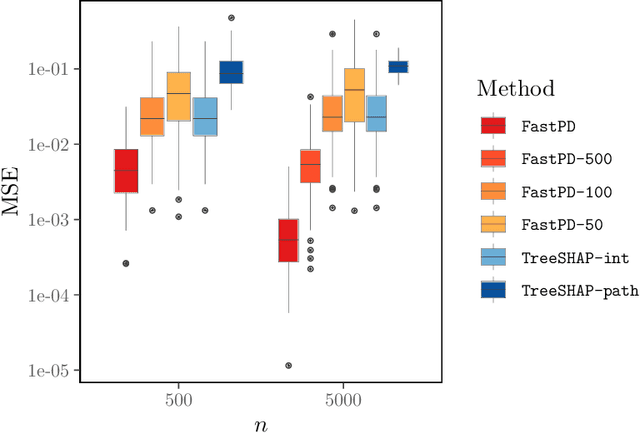
Many existing interpretation methods are based on Partial Dependence (PD) functions that, for a pre-trained machine learning model, capture how a subset of the features affects the predictions by averaging over the remaining features. Notable methods include Shapley additive explanations (SHAP) which computes feature contributions based on a game theoretical interpretation and PD plots (i.e., 1-dim PD functions) that capture average marginal main effects. Recent work has connected these approaches using a functional decomposition and argues that SHAP values can be misleading since they merge main and interaction effects into a single local effect. A major advantage of SHAP compared to other PD-based interpretations, however, has been the availability of fast estimation techniques, such as \texttt{TreeSHAP}. In this paper, we propose a new tree-based estimator, \texttt{FastPD}, which efficiently estimates arbitrary PD functions. We show that \texttt{FastPD} consistently estimates the desired population quantity -- in contrast to path-dependent \texttt{TreeSHAP} which is inconsistent when features are correlated. For moderately deep trees, \texttt{FastPD} improves the complexity of existing methods from quadratic to linear in the number of observations. By estimating PD functions for arbitrary feature subsets, \texttt{FastPD} can be used to extract PD-based interpretations such as SHAP, PD plots and higher order interaction effects.

Hidden Variables unseen by Random Forests

Random Forests are widely claimed to capture interactions well. However, some simple examples suggest that they perform poorly in the presence of certain pure interactions that the conventional CART criterion struggles to capture during tree construction. We argue that simple alternative partitioning schemes used in the tree growing procedure can enhance identification of these interactions. In a simulation study we compare these variants to conventional Random Forests and Extremely Randomized trees. Our results validate that the modifications considered enhance the model's fitting ability in scenarios where pure interactions play a crucial role.

Unifying local and global model explanations by functional decomposition of low dimensional structures

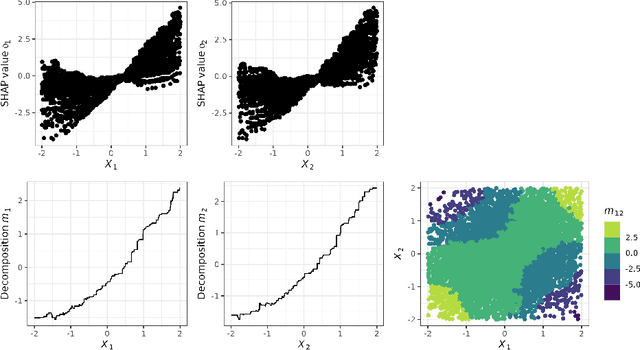
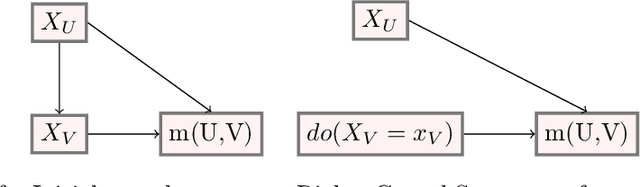
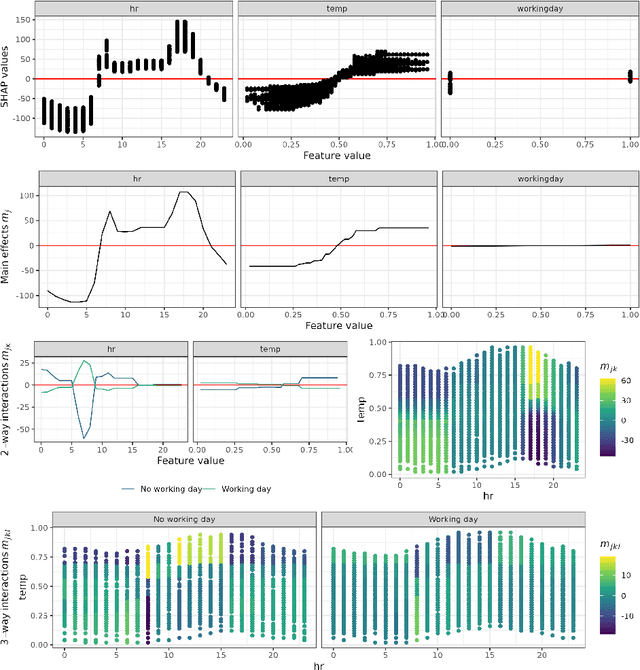
We consider a global explanation of a regression or classification function by decomposing it into the sum of main components and interaction components of arbitrary order. When adding an identification constraint that is motivated by a causal interpretation, we find q-interaction SHAP to be the unique solution to that constraint. Here, q denotes the highest order of interaction present in the decomposition. Our result provides a new perspective on SHAP values with various practical and theoretical implications: If SHAP values are decomposed into main and all interaction effects, they provide a global explanation with causal interpretation. In principle, the decomposition can be applied to any machine learning model. However, since the number of possible interactions grows exponentially with the number of features, exact calculation is only feasible for methods that fit low dimensional structures or ensembles of those. We provide an algorithm and efficient implementation for gradient boosted trees (xgboost and random planted forests that calculates this decomposition. Conducted experiments suggest that our method provides meaningful explanations and reveals interactions of higher orders. We also investigate further potential of our new insights by utilizing the global explanation for motivating a new measure of feature importance, and for reducing direct and indirect bias by post-hoc component removal.

Random Planted Forest: a directly interpretable tree ensemble

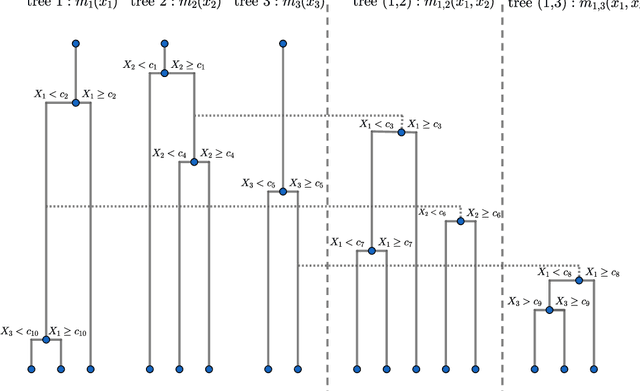
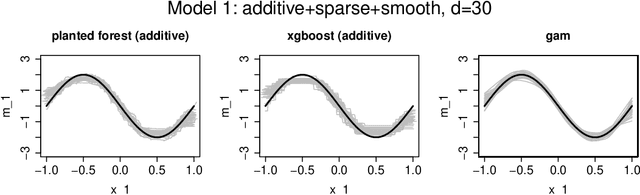
We introduce a novel interpretable and tree-based algorithm for prediction in a regression setting in which each tree in a classical random forest is replaced by a family of planted trees that grow simultaneously. The motivation for our algorithm is to estimate the unknown regression function from a functional ANOVA decomposition perspective, where each tree corresponds to a function within that decomposition. Therefore, planted trees are limited in the number of interaction terms. The maximal order of approximation in the ANOVA decomposition can be specified or left unlimited. If a first order approximation is chosen, the result is an additive model. In the other extreme case, if the order of approximation is not limited, the resulting model puts no restrictions on the form of the regression function. In a simulation study we find encouraging prediction and visualisation properties of our random planted forest method. We also develop theory for an idealised version of random planted forests in the case of an underlying additive model. We show that in the additive case, the idealised version achieves up to a logarithmic factor asymptotically optimal one-dimensional convergence rates of order $n^{-2/5}$.