Hidden Variables unseen by Random Forests

Random Forests are widely claimed to capture interactions well. However, some simple examples suggest that they perform poorly in the presence of certain pure interactions that the conventional CART criterion struggles to capture during tree construction. We argue that simple alternative partitioning schemes used in the tree growing procedure can enhance identification of these interactions. In a simulation study we compare these variants to conventional Random Forests and Extremely Randomized trees. Our results validate that the modifications considered enhance the model's fitting ability in scenarios where pure interactions play a crucial role.

Random Planted Forest: a directly interpretable tree ensemble

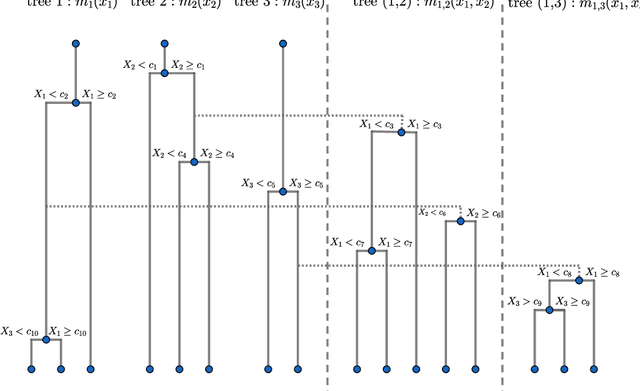
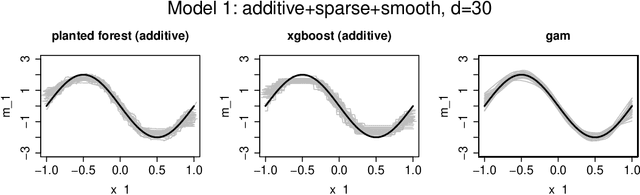
We introduce a novel interpretable and tree-based algorithm for prediction in a regression setting in which each tree in a classical random forest is replaced by a family of planted trees that grow simultaneously. The motivation for our algorithm is to estimate the unknown regression function from a functional ANOVA decomposition perspective, where each tree corresponds to a function within that decomposition. Therefore, planted trees are limited in the number of interaction terms. The maximal order of approximation in the ANOVA decomposition can be specified or left unlimited. If a first order approximation is chosen, the result is an additive model. In the other extreme case, if the order of approximation is not limited, the resulting model puts no restrictions on the form of the regression function. In a simulation study we find encouraging prediction and visualisation properties of our random planted forest method. We also develop theory for an idealised version of random planted forests in the case of an underlying additive model. We show that in the additive case, the idealised version achieves up to a logarithmic factor asymptotically optimal one-dimensional convergence rates of order $n^{-2/5}$.