Responsibility-aware Strategic Reasoning in Probabilistic Multi-Agent Systems

Responsibility plays a key role in the development and deployment of trustworthy autonomous systems. In this paper, we focus on the problem of strategic reasoning in probabilistic multi-agent systems with responsibility-aware agents. We introduce the logic PATL+R, a variant of Probabilistic Alternating-time Temporal Logic. The novelty of PATL+R lies in its incorporation of modalities for causal responsibility, providing a framework for responsibility-aware multi-agent strategic reasoning. We present an approach to synthesise joint strategies that satisfy an outcome specified in PATL+R, while optimising the share of expected causal responsibility and reward. This provides a notion of balanced distribution of responsibility and reward gain among agents. To this end, we utilise the Nash equilibrium as the solution concept for our strategic reasoning problem and demonstrate how to compute responsibility-aware Nash equilibrium strategies via a reduction to parametric model checking of concurrent stochastic multi-player games.

Synthesis of Reward Machines for Multi-Agent Equilibrium Design (Full Version)

Mechanism design is a well-established game-theoretic paradigm for designing games to achieve desired outcomes. This paper addresses a closely related but distinct concept, equilibrium design. Unlike mechanism design, the designer's authority in equilibrium design is more constrained; she can only modify the incentive structures in a given game to achieve certain outcomes without the ability to create the game from scratch. We study the problem of equilibrium design using dynamic incentive structures, known as reward machines. We use weighted concurrent game structures for the game model, with goals (for the players and the designer) defined as mean-payoff objectives. We show how reward machines can be used to represent dynamic incentives that allocate rewards in a manner that optimises the designer's goal. We also introduce the main decision problem within our framework, the payoff improvement problem. This problem essentially asks whether there exists a dynamic incentive (represented by some reward machine) that can improve the designer's payoff by more than a given threshold value. We present two variants of the problem: strong and weak. We demonstrate that both can be solved in polynomial time using a Turing machine equipped with an NP oracle. Furthermore, we also establish that these variants are either NP-hard or coNP-hard. Finally, we show how to synthesise the corresponding reward machine if it exists.

On the Complexity of Rational Verification

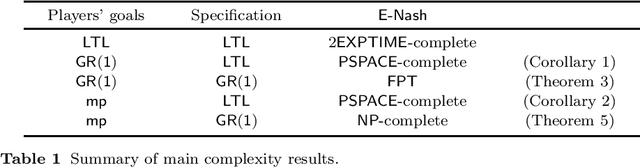
Rational verification refers to the problem of checking which temporal logic properties hold of a concurrent multiagent system, under the assumption that agents in the system choose strategies that form a game-theoretic equilibrium. Rational verification can be understood as a counterpart to model checking for multiagent systems, but while classical model checking can be done in polynomial time for some temporal logic specification languages such as CTL, and polynomial space with LTL specifications, rational verification is much harder: the key decision problems for rational verification are 2EXPTIME-complete with LTL specifications, even when using explicit-state system representations. Against this background, our contributions in this paper are threefold. First, we show that the complexity of rational verification can be greatly reduced by restricting specifications to GR(1), a fragment of LTL that can represent a broad and practically useful class of response properties of reactive systems. In particular, we show that for a number of relevant settings, rational verification can be done in polynomial space and even in polynomial time. Second, we provide improved complexity results for rational verification when considering players' goals given by mean-payoff utility functions; arguably the most widely used approach for quantitative objectives in concurrent and multiagent systems. Finally, we consider the problem of computing outcomes that satisfy social welfare constraints. To this end, we consider both utilitarian and egalitarian social welfare and show that computing such outcomes is either PSPACE-complete or NP-complete.

Rational Verification for Probabilistic Systems

Rational verification is the problem of determining which temporal logic properties will hold in a multi-agent system, under the assumption that agents in the system act rationally, by choosing strategies that collectively form a game-theoretic equilibrium. Previous work in this area has largely focussed on deterministic systems. In this paper, we develop the theory and algorithms for rational verification in probabilistic systems. We focus on concurrent stochastic games (CSGs), which can be used to model uncertainty and randomness in complex multi-agent environments. We study the rational verification problem for both non-cooperative games and cooperative games in the qualitative probabilistic setting. In the former case, we consider LTL properties satisfied by the Nash equilibria of the game and in the latter case LTL properties satisfied by the core. In both cases, we show that the problem is 2EXPTIME-complete, thus not harder than the much simpler verification problem of model checking LTL properties of systems modelled as Markov decision processes (MDPs).

Equilibrium Design for Concurrent Games

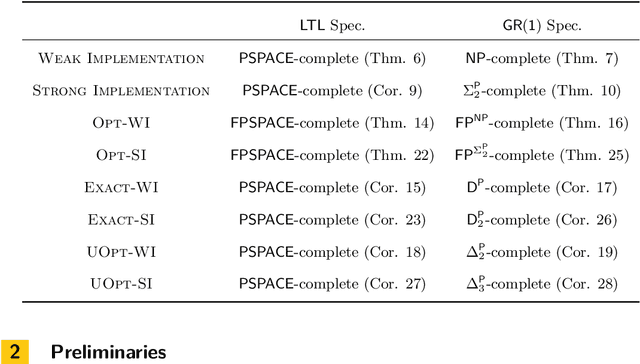
In game theory, mechanism design is concerned with the design of incentives so that a desired outcome of the game can be achieved. In this paper, we study the design of incentives so that a desirable equilibrium is obtained, for instance, an equilibrium satisfying a given temporal logic property -- a problem that we call equilibrium design. We base our study on a framework where system specifications are represented as temporal logic formulae, games as quantitative concurrent game structures, and players' goals as mean-payoff objectives. In particular, we consider system specifications given by LTL and GR(1) formulae, and show that implementing a mechanism to ensure that a given temporal logic property is satisfied on some/every Nash equilibrium of the game, whenever such a mechanism exists, can be done in PSPACE for LTL properties and in NP/$\Sigma^{P}_{2}$ for GR(1) specifications. We also study the complexity of various related decision and optimisation problems, such as optimality and uniqueness of solutions, and show that the complexities of all such problems lie within the polynomial hierarchy. As an application, equilibrium design can be used as an alternative solution to the rational synthesis and verification problems for concurrent games with mean-payoff objectives whenever no solution exists, or as a technique to repair, whenever possible, concurrent games with undesirable rational outcomes (Nash equilibria) in an optimal way.

Automated Temporal Equilibrium Analysis: Verification and Synthesis of Multi-Player Games

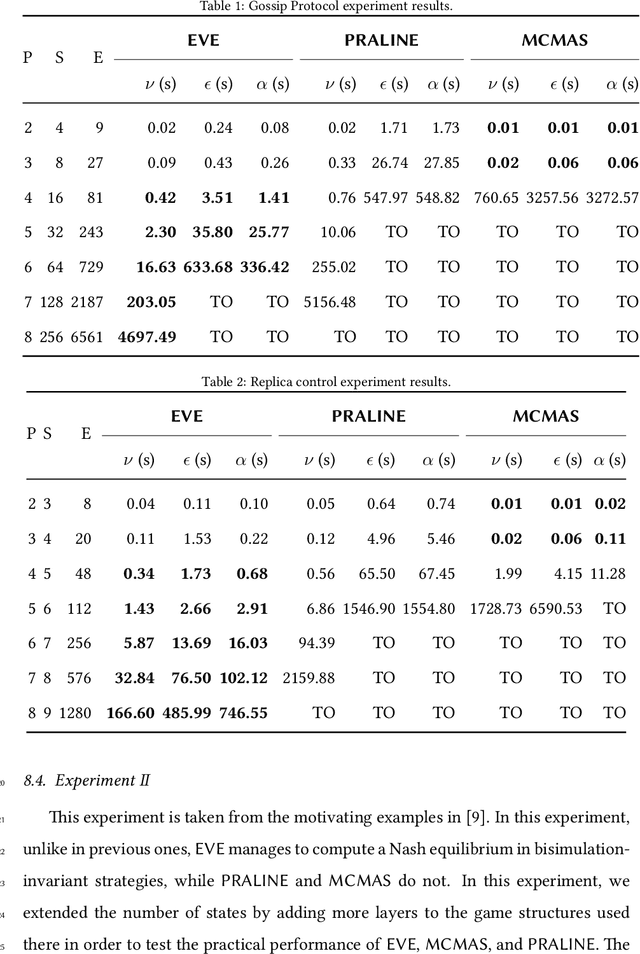
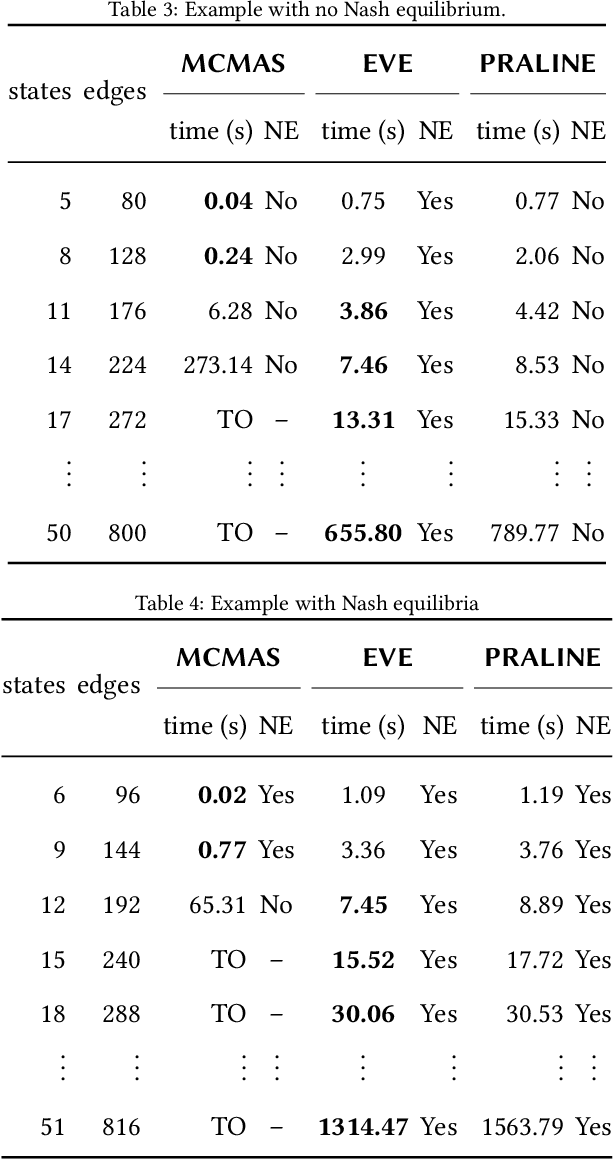
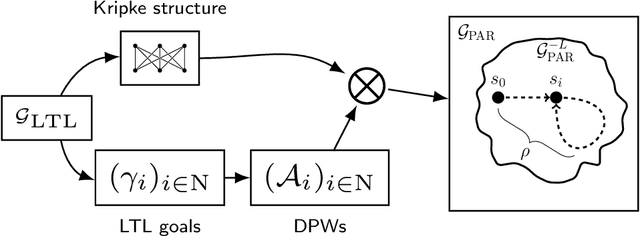
In the context of multi-agent systems, the rational verification problem is concerned with checking which temporal logic properties will hold in a system when its constituent agents are assumed to behave rationally and strategically in pursuit of individual objectives. Typically, those objectives are expressed as temporal logic formulae which the relevant agent desires to see satisfied. Unfortunately, rational verification is computationally complex, and requires specialised techniques in order to obtain practically useable implementations. In this paper, we present such a technique. This technique relies on a reduction of the rational verification problem to the solution of a collection of parity games. Our approach has been implemented in the Equilibrium Verification Environment (EVE) system. The EVE system takes as input a model of a concurrent/multi-agent system represented using the Simple Reactive Modules Language (SRML), where agent goals are represented as Linear Temporal Logic (LTL) formulae, together with a claim about the equilibrium behaviour of the system, also expressed as an LTL formula. EVE can then check whether the LTL claim holds on some (or every) computation of the system that could arise through agents choosing Nash equilibrium strategies; it can also check whether a system has a Nash equilibrium, and synthesise individual strategies for players in the multi-player game. After presenting our basic framework, we describe our new technique and prove its correctness. We then describe our implementation in the EVE system, and present experimental results which show that EVE performs favourably in comparison to other existing tools that support rational verification.