Learning Differentiable Tensegrity Dynamics using Graph Neural Networks

Tensegrity robots are composed of rigid struts and flexible cables. They constitute an emerging class of hybrid rigid-soft robotic systems and are promising systems for a wide array of applications, ranging from locomotion to assembly. They are difficult to control and model accurately, however, due to their compliance and high number of degrees of freedom. To address this issue, prior work has introduced a differentiable physics engine designed for tensegrity robots based on first principles. In contrast, this work proposes the use of graph neural networks to model contact dynamics over a graph representation of tensegrity robots, which leverages their natural graph-like cable connectivity between end caps of rigid rods. This learned simulator can accurately model 3-bar and 6-bar tensegrity robot dynamics in simulation-to-simulation experiments where MuJoCo is used as the ground truth. It can also achieve higher accuracy than the previous differentiable engine for a real 3-bar tensegrity robot, for which the robot state is only partially observable. When compared against direct applications of recent mesh-based graph neural network simulators, the proposed approach is computationally more efficient, both for training and inference, while achieving higher accuracy. Code and data are available at https://github.com/nchen9191/tensegrity_gnn_simulator_public

Real2Sim2Real Transfer for Control of Cable-driven Robots via a Differentiable Physics Engine

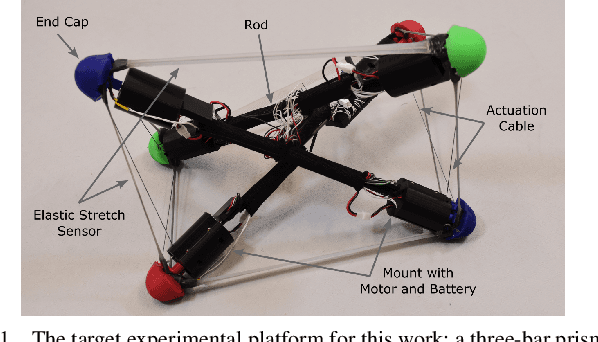
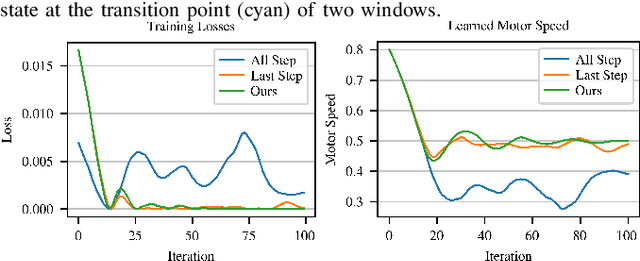
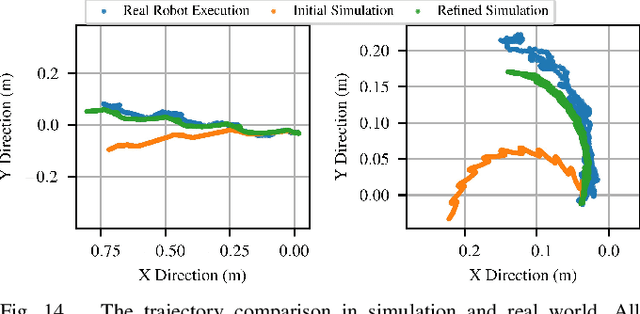
Tensegrity robots, composed of rigid rods and flexible cables, exhibit high strength-to-weight ratios and extreme deformations, enabling them to navigate unstructured terrain and even survive harsh impacts. However, they are hard to control due to their high dimensionality, complex dynamics, and coupled architecture. Physics-based simulation is one avenue for developing locomotion policies that can then be transferred to real robots, but modeling tensegrity robots is a complex task, so simulations experience a substantial sim2real gap. To address this issue, this paper describes a Real2Sim2Real strategy for tensegrity robots. This strategy is based on a differential physics engine that can be trained given limited data from a real robot (i.e. offline measurements and one random trajectory) and achieve a high enough accuracy to discover transferable locomotion policies. Beyond the overall pipeline, key contributions of this work include computing non-zero gradients at contact points, a loss function, and a trajectory segmentation technique that avoid conflicts in gradient evaluation during training. The proposed pipeline is demonstrated and evaluated on a real 3-bar tensegrity robot.

A Recurrent Differentiable Engine for Modeling Tensegrity Robots Trainable with Low-Frequency Data

Tensegrity robots, composed of rigid rods and flexible cables, are difficult to accurately model and control given the presence of complex dynamics and high number of DoFs. Differentiable physics engines have been recently proposed as a data-driven approach for model identification of such complex robotic systems. These engines are often executed at a high-frequency to achieve accurate simulation. Ground truth trajectories for training differentiable engines, however, are not typically available at such high frequencies due to limitations of real-world sensors. The present work focuses on this frequency mismatch, which impacts the modeling accuracy. We proposed a recurrent structure for a differentiable physics engine of tensegrity robots, which can be trained effectively even with low-frequency trajectories. To train this new recurrent engine in a robust way, this work introduces relative to prior work: (i) a new implicit integration scheme, (ii) a progressive training pipeline, and (iii) a differentiable collision checker. A model of NASA's icosahedron SUPERballBot on MuJoCo is used as the ground truth system to collect training data. Simulated experiments show that once the recurrent differentiable engine has been trained given the low-frequency trajectories from MuJoCo, it is able to match the behavior of MuJoCo's system. The criterion for success is whether a locomotion strategy learned using the differentiable engine can be transferred back to the ground-truth system and result in a similar motion. Notably, the amount of ground truth data needed to train the differentiable engine, such that the policy is transferable to the ground truth system, is 1% of the data needed to train the policy directly on the ground-truth system.

An End-to-End Differentiable but Explainable Physics Engine for Tensegrity Robots: Modeling and Control

This work proposes an end-to-end differentiable physics engine for tensegrity robots, which introduces a data-efficient linear contact model for accurately predicting collision responses that arise due to contacting surfaces, and a linear actuator model that can drive these robots by expanding and contracting their flexible cables. To the best of the authors' knowledge, this is the \emph{first} differentiable physics engine for tensegrity robots that supports cable modeling, contact, and actuation. This engine can be used inside an off-the-shelf, RL-based locomotion controller in order to provide training examples. This paper proposes a progressive training pipeline for the differentiable physics engine that helps avoid local optima during the training phase and reduces data requirements. It demonstrates the data-efficiency benefits of using the differentiable engine for learning locomotion policies for NASA's icosahedron SUPERballBot. In particular, after the engine has been trained with few trajectories to match a ground truth simulated model, then a policy learned on the differentiable engine is shown to be transferable back to the ground-truth model. Training the controller requires orders of magnitude more data than training the differential engine.

Spring-Rod System Identification via Differentiable Physics Engine

We propose a novel differentiable physics engine for system identification of complex spring-rod assemblies. Unlike black-box data-driven methods for learning the evolution of a dynamical system \emph{and} its parameters, we modularize the design of our engine using a discrete form of the governing equations of motion, similar to a traditional physics engine. We further reduce the dimension from 3D to 1D for each module, which allows efficient learning of system parameters using linear regression. The regression parameters correspond to physical quantities, such as spring stiffness or the mass of the rod, making the pipeline explainable. The approach significantly reduces the amount of training data required, and also avoids iterative identification of data sampling and model training. We compare the performance of the proposed engine with previous solutions, and demonstrate its efficacy on tensegrity systems, such as NASA's icosahedron.

Model Identification and Control of a Low-Cost Wheeled Mobile Robot Using Differentiable Physics

We present the design of a low-cost wheeled mobile robot, and an analytical model for predicting its motion under the influence of motor torques and friction forces. Using our proposed model, we show how to analytically compute the gradient of an appropriate loss function, that measures the deviation between predicted motion trajectories and real-world trajectories, which are estimated using Apriltags and an overhead camera. These analytical gradients allow us to automatically infer the unknown friction coefficients, by minimizing the loss function using gradient descent. Motion trajectories that are predicted by the optimized model are in excellent agreement with their real-world counterparts. Experiments show that our proposed approach is computationally superior to existing black-box system identification methods and other data-driven techniques, and also requires very few real-world samples for accurate trajectory prediction. The proposed approach combines the data efficiency of analytical models based on first principles, with the flexibility of data-driven methods, which makes it appropriate for low-cost robots. Using the learned model and our gradient-based optimization approach, we show how to automatically compute motor control signals for driving the robot along pre-specified curves.

A First Principles Approach for Data-Efficient System Identification of Spring-Rod Systems via Differentiable Physics Engines

We propose a novel differentiable physics engine for system identification of complex spring-rod assemblies. Unlike black-box data-driven methods for learning the evolution of a dynamical system and its parameters, we modularize the design of our engine using a discrete form of the governing equations of motion, similar to a traditional physics engine. We further reduce the dimension from 3D to 1D for each module, which allows efficient learning of system parameters using linear regression. As a side benefit, the regression parameters correspond to physical quantities, such as spring stiffness or the mass of the rod, making the pipeline explainable. The approach significantly reduces the amount of training data required, and also avoids iterative identification of data sampling and model training. We compare the performance of the proposed engine with previous solutions, and demonstrate its efficacy on tensegrity systems, such as NASA's icosahedron.