Predicting the State of Synchronization of Financial Time Series using Cross Recurrence Plots

Cross-correlation analysis is a powerful tool for understanding the mutual dynamics of time series. This study introduces a new method for predicting the future state of synchronization of the dynamics of two financial time series. To this end, we use the cross-recurrence plot analysis as a nonlinear method for quantifying the multidimensional coupling in the time domain of two time series and for determining their state of synchronization. We adopt a deep learning framework for methodologically addressing the prediction of the synchronization state based on features extracted from dynamically sub-sampled cross-recurrence plots. We provide extensive experiments on several stocks, major constituents of the S\&P100 index, to empirically validate our approach. We find that the task of predicting the state of synchronization of two time series is in general rather difficult, but for certain pairs of stocks attainable with very satisfactory performance.

Exact Manifold Gaussian Variational Bayes

We propose an optimization algorithm for Variational Inference (VI) in complex models. Our approach relies on natural gradient updates where the variational space is a Riemann manifold. We develop an efficient algorithm for Gaussian Variational Inference that implicitly satisfies the positive definite constraint on the variational covariance matrix. Our Exact manifold Gaussian Variational Bayes (EMGVB) provides exact but simple update rules and is straightforward to implement. Due to its black-box nature, EMGVB stands as a ready-to-use solution for VI in complex models. Over five datasets, we empirically validate our feasible approach on different statistical, econometric, and deep learning models, discussing its performance with respect to baseline methods.

Augmented Bilinear Network for Incremental Multi-Stock Time-Series Classification

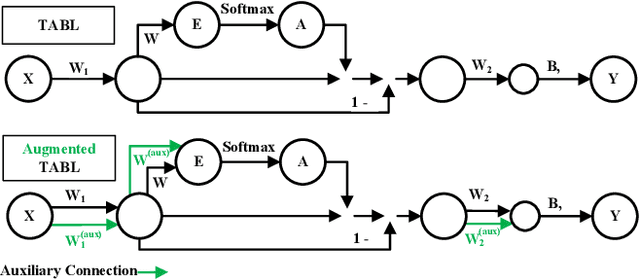
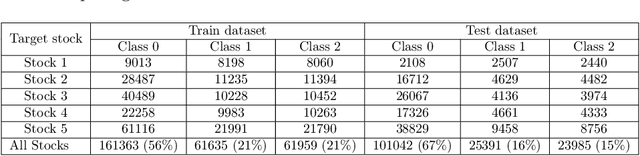
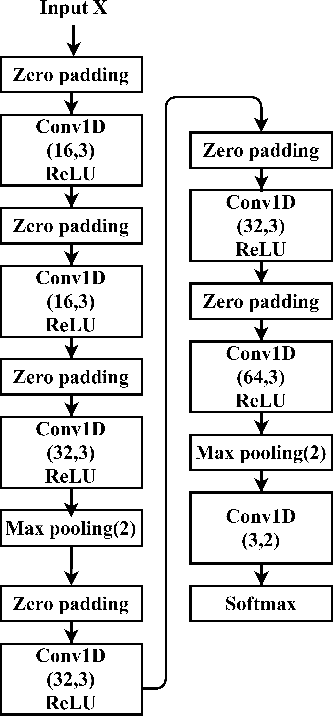
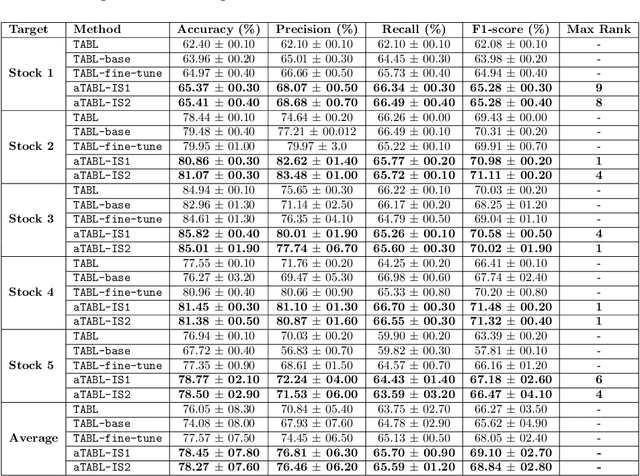
Deep Learning models have become dominant in tackling financial time-series analysis problems, overturning conventional machine learning and statistical methods. Most often, a model trained for one market or security cannot be directly applied to another market or security due to differences inherent in the market conditions. In addition, as the market evolves through time, it is necessary to update the existing models or train new ones when new data is made available. This scenario, which is inherent in most financial forecasting applications, naturally raises the following research question: How to efficiently adapt a pre-trained model to a new set of data while retaining performance on the old data, especially when the old data is not accessible? In this paper, we propose a method to efficiently retain the knowledge available in a neural network pre-trained on a set of securities and adapt it to achieve high performance in new ones. In our method, the prior knowledge encoded in a pre-trained neural network is maintained by keeping existing connections fixed, and this knowledge is adjusted for the new securities by a set of augmented connections, which are optimized using the new data. The auxiliary connections are constrained to be of low rank. This not only allows us to rapidly optimize for the new task but also reduces the storage and run-time complexity during the deployment phase. The efficiency of our approach is empirically validated in the stock mid-price movement prediction problem using a large-scale limit order book dataset. Experimental results show that our approach enhances prediction performance as well as reduces the overall number of network parameters.

Quasi Black-Box Variational Inference with Natural Gradients for Bayesian Learning

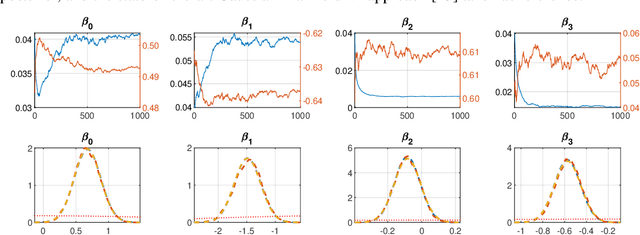
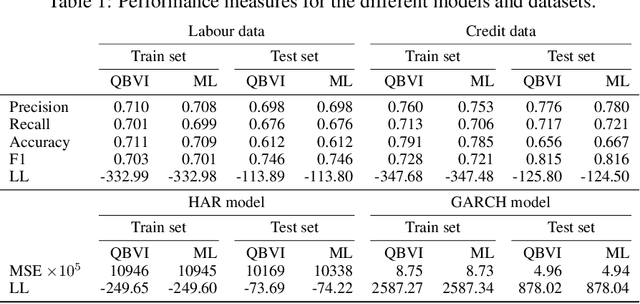
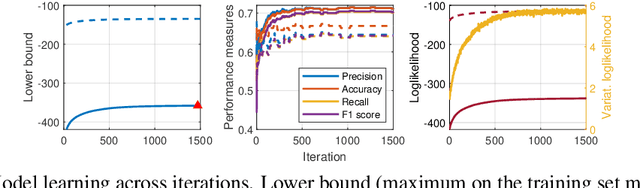
We develop an optimization algorithm suitable for Bayesian learning in complex models. Our approach relies on natural gradient updates within a general black-box framework for efficient training with limited model-specific derivations. It applies within the class of exponential-family variational posterior distributions, for which we extensively discuss the Gaussian case for which the updates have a rather simple form. Our Quasi Black-box Variational Inference (QBVI) framework is readily applicable to a wide class of Bayesian inference problems and is of simple implementation as the updates of the variational posterior do not involve gradients with respect to the model parameters, nor the prescription of the Fisher information matrix. We develop QBVI under different hypotheses for the posterior covariance matrix, discuss details about its robust and feasible implementation, and provide a number of real-world applications to demonstrate its effectiveness.

Bayesian Bilinear Neural Network for Predicting the Mid-price Dynamics in Limit-Order Book Markets

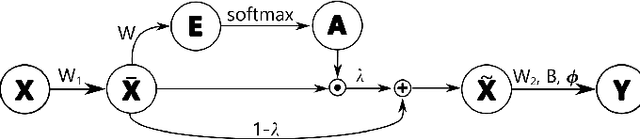
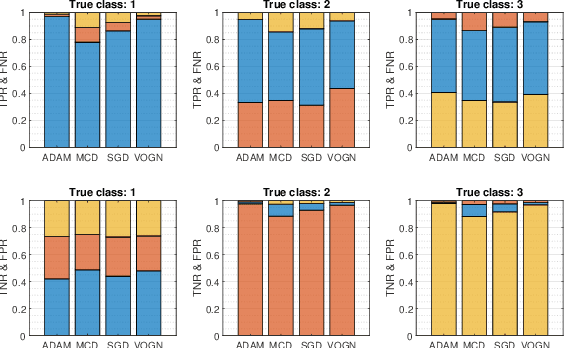
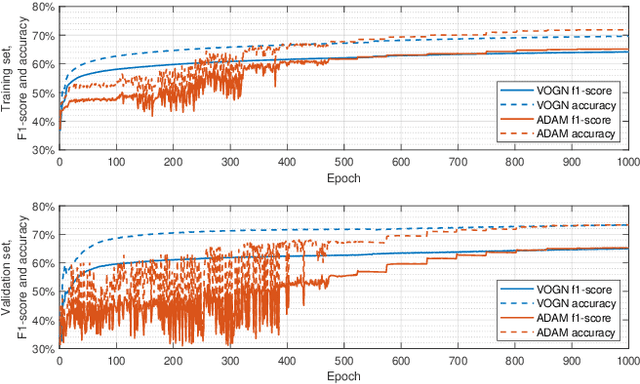
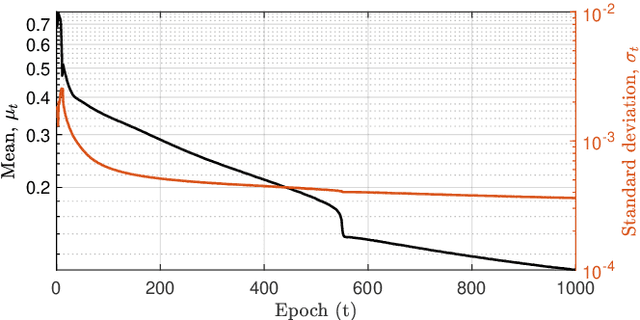
The prediction of financial markets is a challenging yet important task. In modern electronically-driven markets traditional time-series econometric methods often appear incapable of capturing the true complexity of the multi-level interactions driving the price dynamics. While recent research has established the effectiveness of traditional machine learning (ML) models in financial applications, their intrinsic inability in dealing with uncertainties, which is a great concern in econometrics research and real business applications, constitutes a major drawback. Bayesian methods naturally appear as a suitable remedy conveying the predictive ability of ML methods with the probabilistically-oriented practice of econometric research. By adopting a state-of-the-art second-order optimization algorithm, we train a Bayesian bilinear neural network with temporal attention, suitable for the challenging time-series task of predicting mid-price movements in ultra-high-frequency limit-order book markets. By addressing the use of predictive distributions to analyze errors and uncertainties associated with the estimated parameters and model forecasts, we thoroughly compare our Bayesian model with traditional ML alternatives. Our results underline the feasibility of the Bayesian deep learning approach and its predictive and decisional advantages in complex econometric tasks, prompting future research in this direction.

Multi-head Temporal Attention-Augmented Bilinear Network for Financial time series prediction

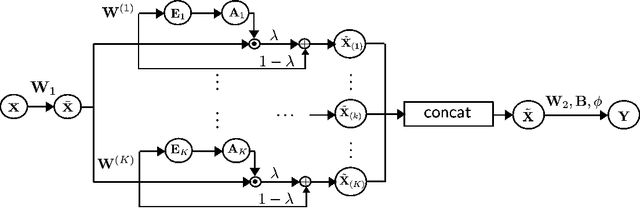
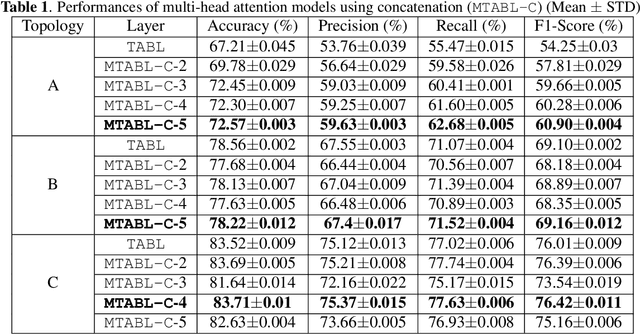
Financial time-series forecasting is one of the most challenging domains in the field of time-series analysis. This is mostly due to the highly non-stationary and noisy nature of financial time-series data. With progressive efforts of the community to design specialized neural networks incorporating prior domain knowledge, many financial analysis and forecasting problems have been successfully tackled. The temporal attention mechanism is a neural layer design that recently gained popularity due to its ability to focus on important temporal events. In this paper, we propose a neural layer based on the ideas of temporal attention and multi-head attention to extend the capability of the underlying neural network in focusing simultaneously on multiple temporal instances. The effectiveness of our approach is validated using large-scale limit-order book market data to forecast the direction of mid-price movements. Our experiments show that the use of multi-head temporal attention modules leads to enhanced prediction performances compared to baseline models.

Low-Rank Temporal Attention-Augmented Bilinear Network for financial time-series forecasting

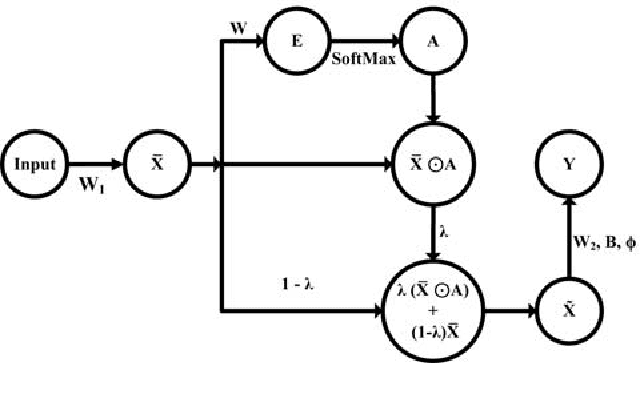
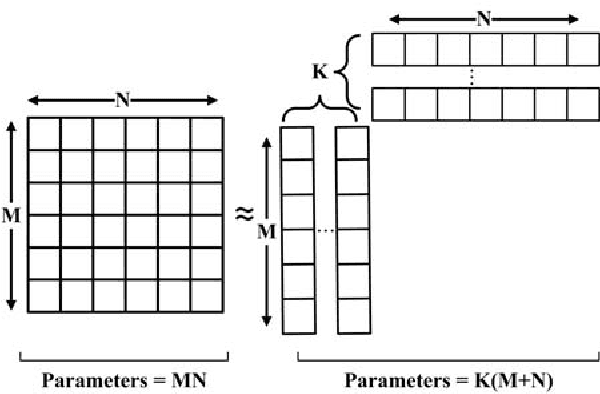
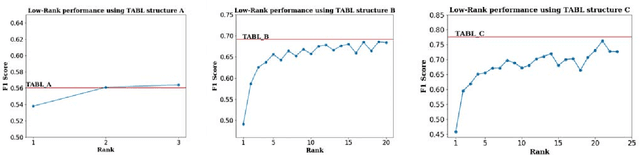
Financial market analysis, especially the prediction of movements of stock prices, is a challenging problem. The nature of financial time-series data, being non-stationary and nonlinear, is the main cause of these challenges. Deep learning models have led to significant performance improvements in many problems coming from different domains, including prediction problems of financial time-series data. Although the prediction performance is the main goal of such models, dealing with ultra high-frequency data sets restrictions in terms of the number of model parameters and its inference speed. The Temporal Attention-Augmented Bilinear network was recently proposed as an efficient and high-performing model for Limit Order Book time-series forecasting. In this paper, we propose a low-rank tensor approximation of the model to further reduce the number of trainable parameters and increase its speed.