Quasi Black-Box Variational Inference with Natural Gradients for Bayesian Learning
Paper and Code
May 23, 2022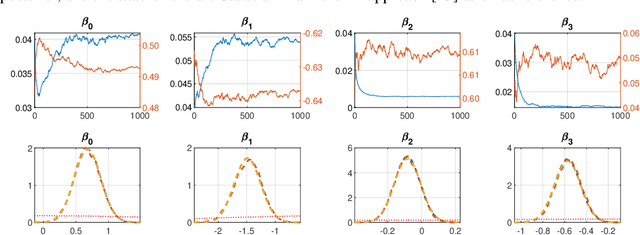
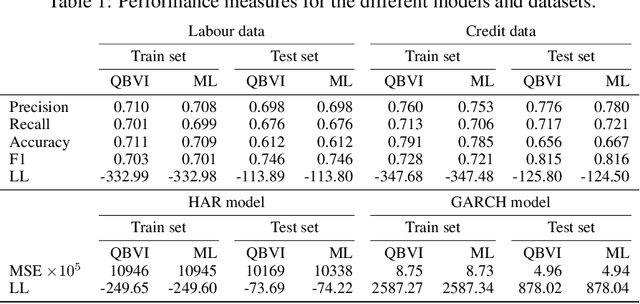
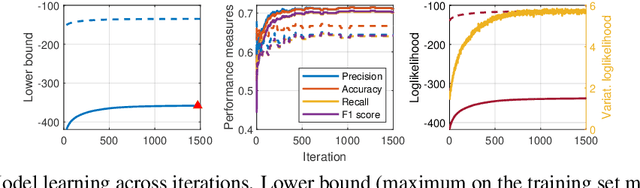
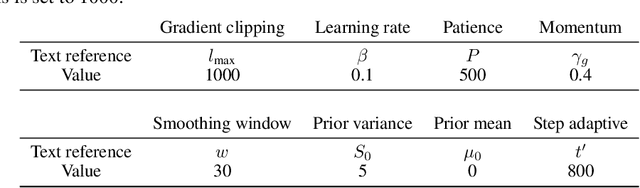
We develop an optimization algorithm suitable for Bayesian learning in complex models. Our approach relies on natural gradient updates within a general black-box framework for efficient training with limited model-specific derivations. It applies within the class of exponential-family variational posterior distributions, for which we extensively discuss the Gaussian case for which the updates have a rather simple form. Our Quasi Black-box Variational Inference (QBVI) framework is readily applicable to a wide class of Bayesian inference problems and is of simple implementation as the updates of the variational posterior do not involve gradients with respect to the model parameters, nor the prescription of the Fisher information matrix. We develop QBVI under different hypotheses for the posterior covariance matrix, discuss details about its robust and feasible implementation, and provide a number of real-world applications to demonstrate its effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge