Multimodal Diffeomorphic Registration with Neural ODEs and Structural Descriptors

This work proposes a multimodal diffeomorphic registration method using Neural Ordinary Differential Equations (Neural ODEs). Nonrigid registration algorithms exhibit tradeoffs between their accuracy, the computational complexity of their deformation model, and its proper regularization. In addition, they also assume intensity correlation in anatomically homologous regions of interest among image pairs, limiting their applicability to the monomodal setting. Unlike learning-based models, we propose an instance-specific framework that is not subject to high scan requirements for training and does not suffer performance degradation at inference time on modalities unseen during training. Our method exploits the potential of continuous-depth networks in the Neural ODE paradigm with structural descriptors, widely adopted as modality-agnostic metric models which exploit self-similarities on parameterized neighborhood geometries. We propose three different variants that integrate image-based or feature-based structural descriptors and nonstructural image similarities computed by local mutual information. We conduct extensive evaluations on different experiments formed by scan dataset combinations and show surpassing qualitative and quantitative results compared to state-of-the-art baselines adequate for large or small deformations, and specific of multimodal registration. Lastly, we also demonstrate the underlying robustness of the proposed framework to varying levels of explicit regularization while maintaining low error, its suitability for registration at varying scales, and its efficiency with respect to other methods targeted to large-deformation registration.

Explainable artificial intelligence toward usable and trustworthy computer-aided early diagnosis of multiple sclerosis from Optical Coherence Tomography

Background: Several studies indicate that the anterior visual pathway provides information about the dynamics of axonal degeneration in Multiple Sclerosis (MS). Current research in the field is focused on the quest for the most discriminative features among patients and controls and the development of machine learning models that yield computer-aided solutions widely usable in clinical practice. However, most studies are conducted with small samples and the models are used as black boxes. Clinicians should not trust machine learning decisions unless they come with comprehensive and easily understandable explanations. Materials and methods: A total of 216 eyes from 111 healthy controls and 100 eyes from 59 patients with relapsing-remitting MS were enrolled. The feature set was obtained from the thickness of the ganglion cell layer (GCL) and the retinal nerve fiber layer (RNFL). Measurements were acquired by the novel Posterior Pole protocol from Spectralis Optical Coherence Tomography (OCT) device. We compared two black-box methods (gradient boosting and random forests) with a glass-box method (explainable boosting machine). Explainability was studied using SHAP for the black-box methods and the scores of the glass-box method. Results: The best-performing models were obtained for the GCL layer. Explainability pointed out to the temporal location of the GCL layer that is usually broken or thinning in MS and the relationship between low thickness values and high probability of MS, which is coherent with clinical knowledge. Conclusions: The insights on how to use explainability shown in this work represent a first important step toward a trustworthy computer-aided solution for the diagnosis of MS with OCT.

LDDMM meets GANs: Generative Adversarial Networks for diffeomorphic registration

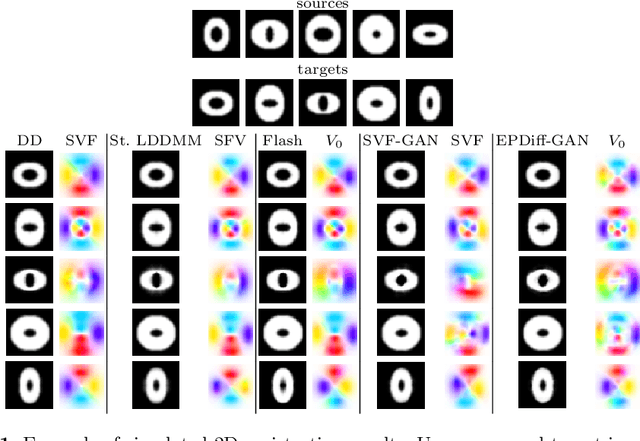
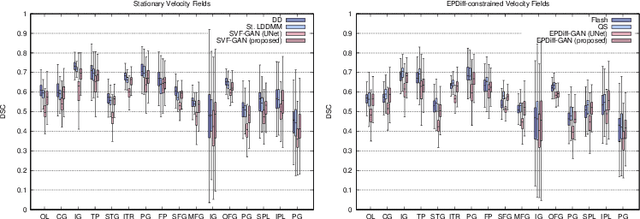
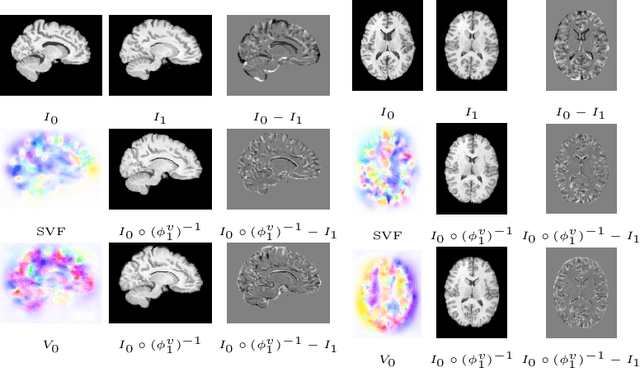
The purpose of this work is to contribute to the state of the art of deep-learning methods for diffeomorphic registration. We propose an adversarial learning LDDMM method for pairs of 3D mono-modal images based on Generative Adversarial Networks. The method is inspired by the recent literature for deformable image registration with adversarial learning. We combine the best performing generative, discriminative, and adversarial ingredients from the state of the art within the LDDMM paradigm. We have successfully implemented two models with the stationary and the EPDiff-constrained non-stationary parameterizations of diffeomorphisms. Our unsupervised and data-hungry approach has shown a competitive performance with respect to a benchmark supervised and rich-data approach. In addition, our method has shown similar results to model-based methods with a computational time under one second.

Combining the band-limited parameterization and Semi-Lagrangian Runge--Kutta integration for efficient PDE-constrained LDDMM

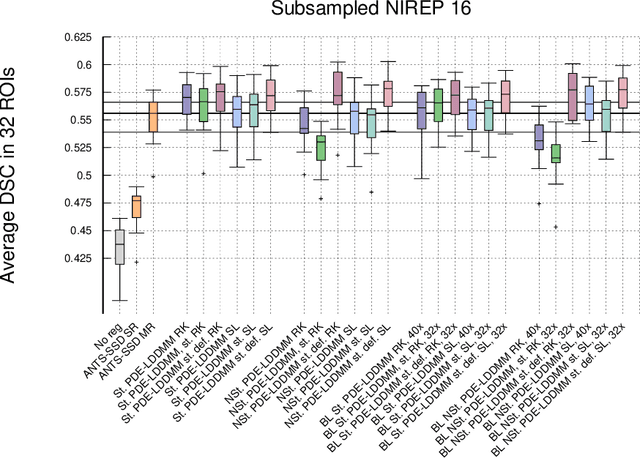
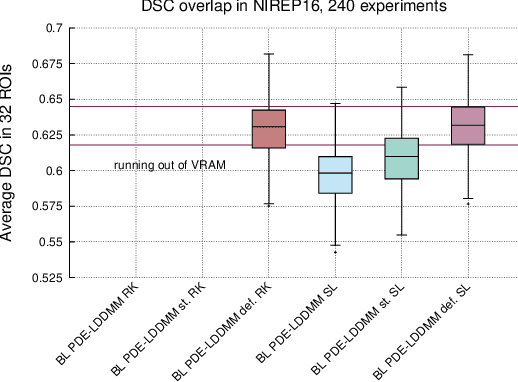
The family of PDE-constrained LDDMM methods is emerging as a particularly interesting approach for physically meaningful diffeomorphic transformations. The original combination of Gauss--Newton--Krylov optimization and Runge--Kutta integration, shows excellent numerical accuracy and fast convergence rate. However, its most significant limitation is the huge computational complexity, hindering its extensive use in Computational Anatomy applied studies. This limitation has been treated independently by the problem formulation in the space of band-limited vector fields and Semi-Lagrangian integration. The purpose of this work is to combine both in three variants of band-limited PDE-constrained LDDMM for further increasing their computational efficiency. The accuracy of the resulting methods is evaluated extensively. For all the variants, the proposed combined approach shows a significant increment of the computational efficiency. In addition, the variant based on the deformation state equation is positioned consistently as the best performing method across all the evaluation frameworks in terms of accuracy and efficiency.

Efficient Gauss-Newton-Krylov momentum conservation constrained PDE-LDDMM using the band-limited vector field parameterization

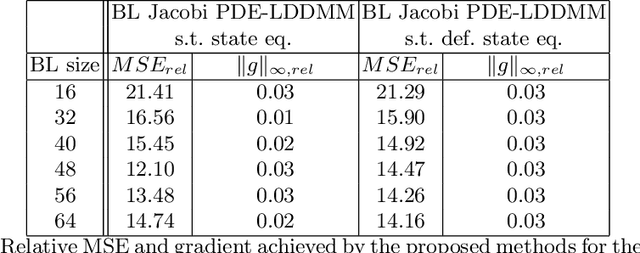
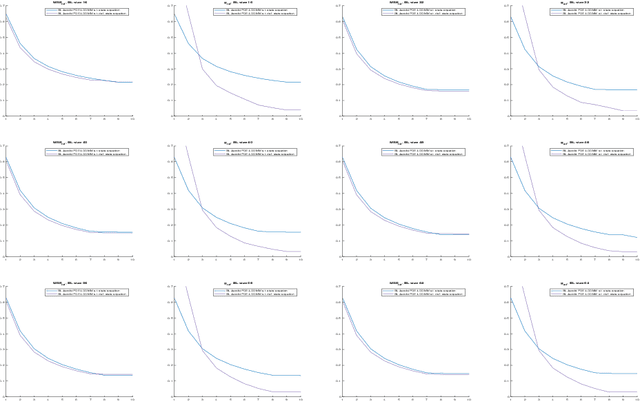
The class of non-rigid registration methods proposed in the framework of PDE-constrained Large Deformation Diffeomorphic Metric Mapping is a particularly interesting family of physically meaningful diffeomorphic registration methods. PDE-constrained LDDMM methods are formulated as constrained variational problems, where the different physical models are imposed using the associated partial differential equations as hard constraints. Inexact Newton-Krylov optimization has shown an excellent numerical accuracy and an extraordinarily fast convergence rate in this framework. However, the Galerkin representation of the non-stationary velocity fields does not provide proper geodesic paths. In a previous work, we proposed a method for PDE-constrained LDDMM parameterized in the space of initial velocity fields under the EPDiff equation. The proposed method provided geodesics in the framework of PDE-constrained LDDMM, and it showed performance competitive to benchmark PDE-constrained LDDMM and EPDiff-LDDMM methods. However, the major drawback of this method was the large memory load inherent to PDE-constrained LDDMM methods and the increased computational time with respect to the benchmark methods. In this work we optimize the computational complexity of the method using the band-limited vector field parameterization closing the loop with our previous works.

Newton-Krylov PDE-constrained LDDMM in the space of band-limited vector fields

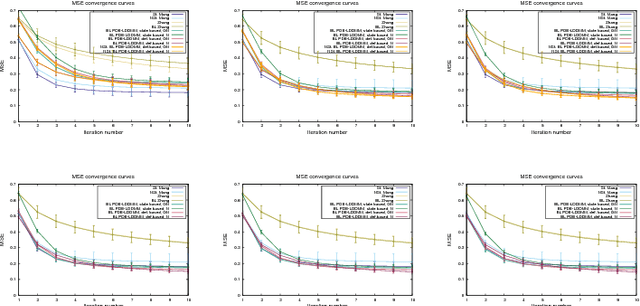
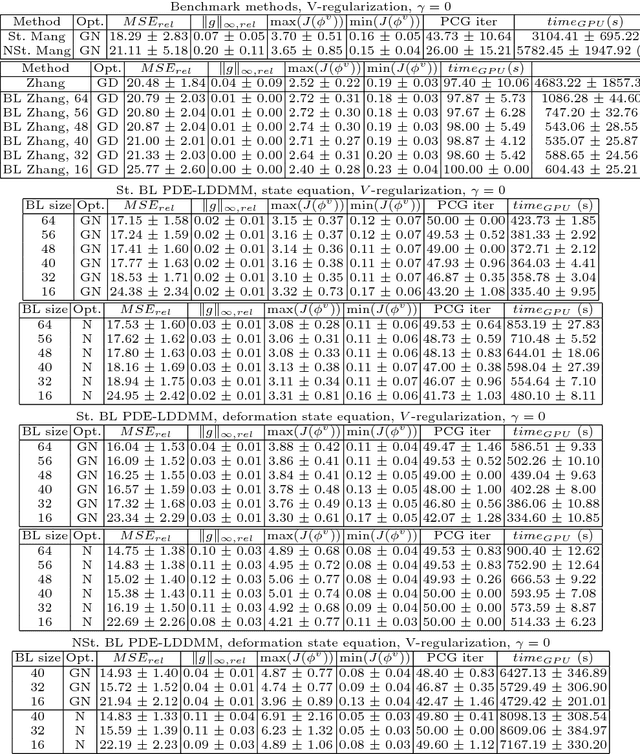
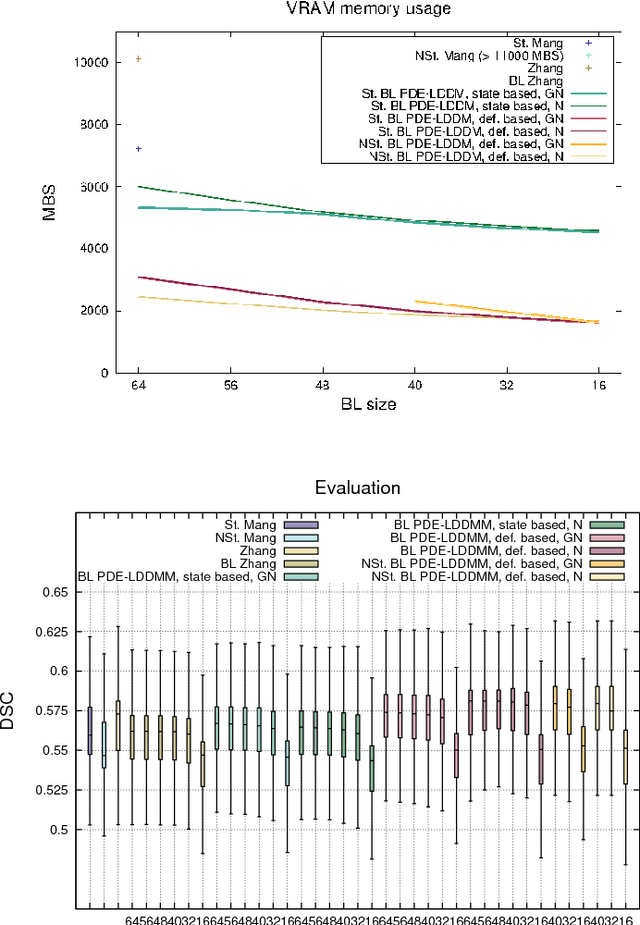
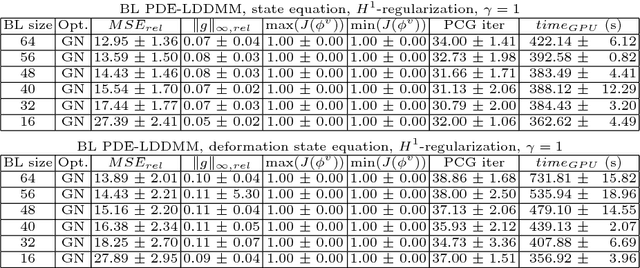
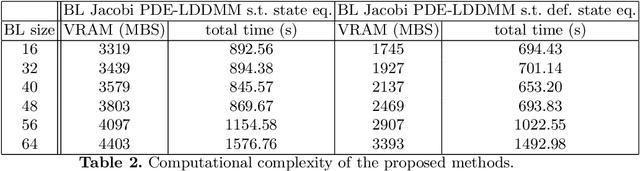
PDE-constrained Large Deformation Diffeomorphic Metric Mapping is a particularly interesting framework of physically meaningful diffeomorphic registration methods. Newton-Krylov optimization has shown an excellent numerical accuracy and an extraordinarily fast convergence rate in this framework. However, the most significant limitation of PDE-constrained LDDMM is the huge computational complexity, that hinders the extensive use in Computational Anatomy applications. In this work, we propose two PDE-constrained LDDMM methods parameterized in the space of band-limited vector fields and we evaluate their performance with respect to the most related state of the art methods. The parameterization in the space of band-limited vector fields dramatically alleviates the computational burden avoiding the computation of the high-frequency components of the velocity fields that would be suppressed by the action of the low-pass filters involved in the computation of the gradient and the Hessian-vector products. Besides, the proposed methods have shown an improved accuracy with respect to the benchmark methods.

PDE-constrained LDDMM via geodesic shooting and inexact Gauss-Newton-Krylov optimization using the incremental adjoint Jacobi equations

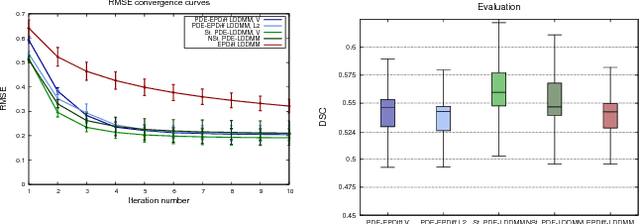
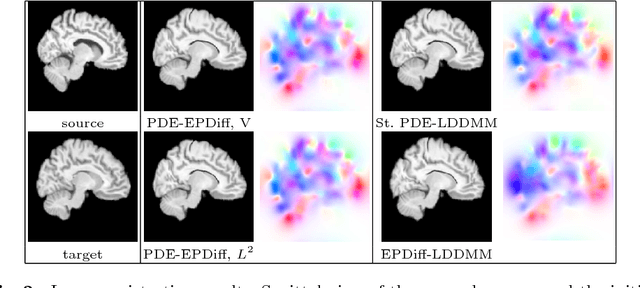
The class of non-rigid registration methods proposed in the framework of PDE-constrained Large Deformation Diffeomorphic Metric Mapping is a particularly interesting family of physically meaningful diffeomorphic registration methods. Inexact Newton-Krylov optimization has shown an excellent numerical accuracy and an extraordinarily fast convergence rate in this framework. However, the Galerkin representation of the non-stationary velocity fields does not provide proper geodesic paths. In this work, we propose a method for PDE-constrained LDDMM parameterized in the space of initial velocity fields under the EPDiff equation. The derivation of the gradient and the Hessian-vector products are performed on the final velocity field and transported backward using the adjoint and the incremental adjoint Jacobi equations. This way, we avoid the complex dependence on the initial velocity field in the derivations and the computation of the adjoint equation and its incremental counterpart. The proposed method provides geodesics in the framework of PDE-constrained LDDMM, and it shows performance competitive to benchmark PDE-constrained LDDMM and EPDiff-LDDMM methods.