Efficient Gauss-Newton-Krylov momentum conservation constrained PDE-LDDMM using the band-limited vector field parameterization
Paper and Code
Jul 27, 2018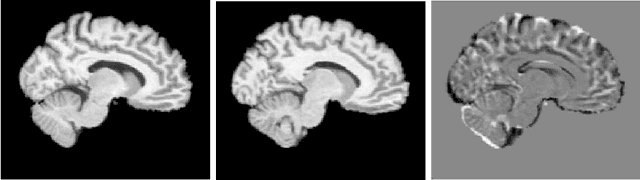
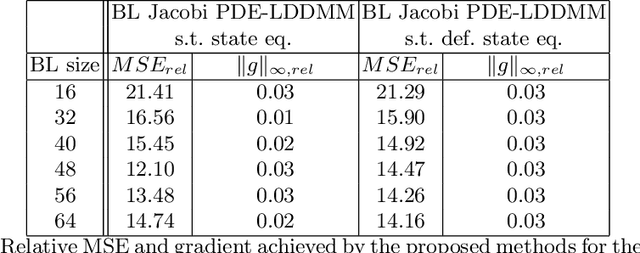
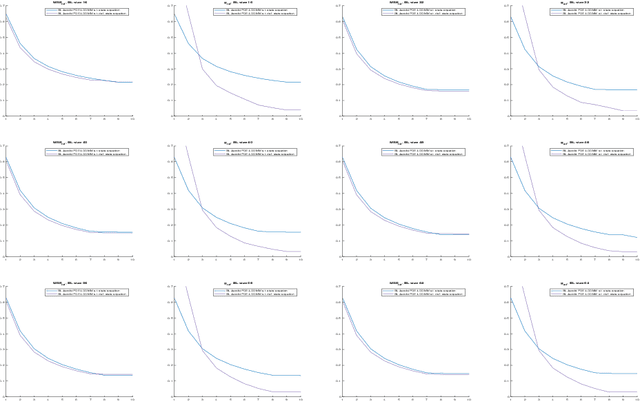
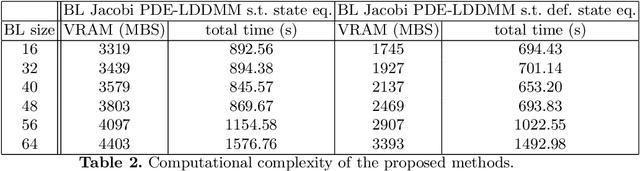
The class of non-rigid registration methods proposed in the framework of PDE-constrained Large Deformation Diffeomorphic Metric Mapping is a particularly interesting family of physically meaningful diffeomorphic registration methods. PDE-constrained LDDMM methods are formulated as constrained variational problems, where the different physical models are imposed using the associated partial differential equations as hard constraints. Inexact Newton-Krylov optimization has shown an excellent numerical accuracy and an extraordinarily fast convergence rate in this framework. However, the Galerkin representation of the non-stationary velocity fields does not provide proper geodesic paths. In a previous work, we proposed a method for PDE-constrained LDDMM parameterized in the space of initial velocity fields under the EPDiff equation. The proposed method provided geodesics in the framework of PDE-constrained LDDMM, and it showed performance competitive to benchmark PDE-constrained LDDMM and EPDiff-LDDMM methods. However, the major drawback of this method was the large memory load inherent to PDE-constrained LDDMM methods and the increased computational time with respect to the benchmark methods. In this work we optimize the computational complexity of the method using the band-limited vector field parameterization closing the loop with our previous works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge