Combining the band-limited parameterization and Semi-Lagrangian Runge--Kutta integration for efficient PDE-constrained LDDMM
Paper and Code
Jun 10, 2020
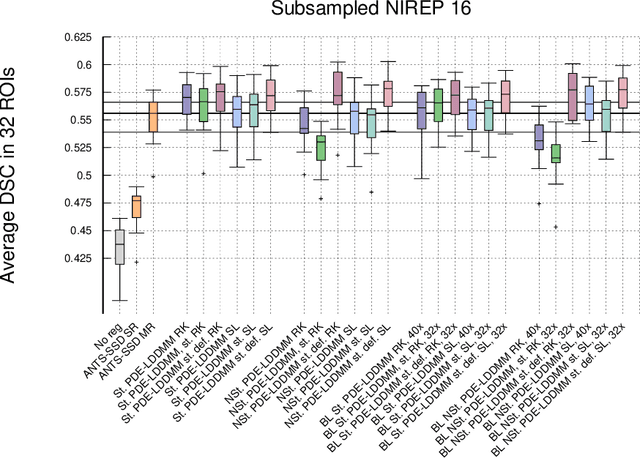
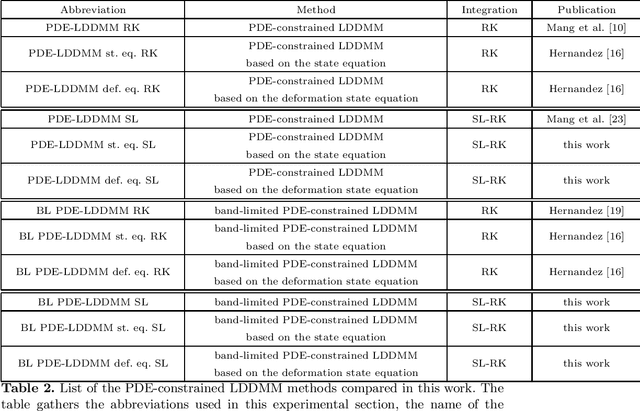
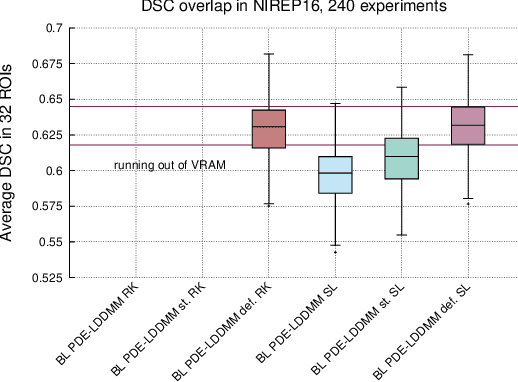
The family of PDE-constrained LDDMM methods is emerging as a particularly interesting approach for physically meaningful diffeomorphic transformations. The original combination of Gauss--Newton--Krylov optimization and Runge--Kutta integration, shows excellent numerical accuracy and fast convergence rate. However, its most significant limitation is the huge computational complexity, hindering its extensive use in Computational Anatomy applied studies. This limitation has been treated independently by the problem formulation in the space of band-limited vector fields and Semi-Lagrangian integration. The purpose of this work is to combine both in three variants of band-limited PDE-constrained LDDMM for further increasing their computational efficiency. The accuracy of the resulting methods is evaluated extensively. For all the variants, the proposed combined approach shows a significant increment of the computational efficiency. In addition, the variant based on the deformation state equation is positioned consistently as the best performing method across all the evaluation frameworks in terms of accuracy and efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge