PDE-constrained LDDMM via geodesic shooting and inexact Gauss-Newton-Krylov optimization using the incremental adjoint Jacobi equations
Paper and Code
Jul 11, 2018
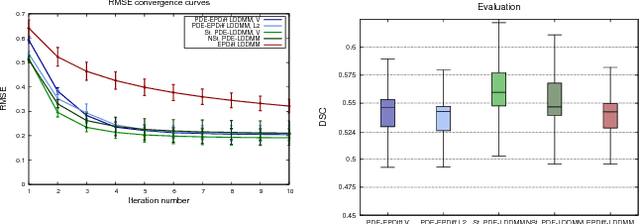
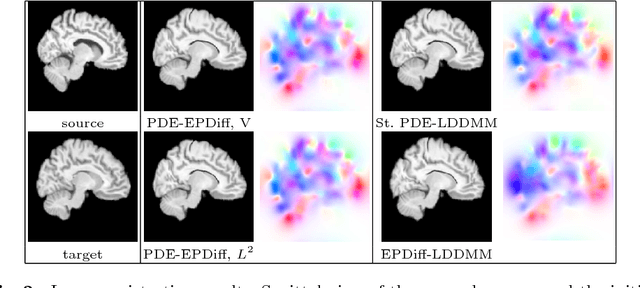
The class of non-rigid registration methods proposed in the framework of PDE-constrained Large Deformation Diffeomorphic Metric Mapping is a particularly interesting family of physically meaningful diffeomorphic registration methods. Inexact Newton-Krylov optimization has shown an excellent numerical accuracy and an extraordinarily fast convergence rate in this framework. However, the Galerkin representation of the non-stationary velocity fields does not provide proper geodesic paths. In this work, we propose a method for PDE-constrained LDDMM parameterized in the space of initial velocity fields under the EPDiff equation. The derivation of the gradient and the Hessian-vector products are performed on the final velocity field and transported backward using the adjoint and the incremental adjoint Jacobi equations. This way, we avoid the complex dependence on the initial velocity field in the derivations and the computation of the adjoint equation and its incremental counterpart. The proposed method provides geodesics in the framework of PDE-constrained LDDMM, and it shows performance competitive to benchmark PDE-constrained LDDMM and EPDiff-LDDMM methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge