Active Learning for Fair and Stable Online Allocations

We explore an active learning approach for dynamic fair resource allocation problems. Unlike previous work that assumes full feedback from all agents on their allocations, we consider feedback from a select subset of agents at each epoch of the online resource allocation process. Despite this restriction, our proposed algorithms provide regret bounds that are sub-linear in number of time-periods for various measures that include fairness metrics commonly used in resource allocation problems and stability considerations in matching mechanisms. The key insight of our algorithms lies in adaptively identifying the most informative feedback using dueling upper and lower confidence bounds. With this strategy, we show that efficient decision-making does not require extensive feedback and produces efficient outcomes for a variety of problem classes.

Information Theoretic Limits for Linear Prediction with Graph-Structured Sparsity

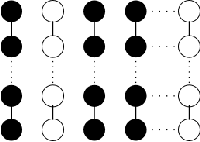
We analyze the necessary number of samples for sparse vector recovery in a noisy linear prediction setup. This model includes problems such as linear regression and classification. We focus on structured graph models. In particular, we prove that sufficient number of samples for the weighted graph model proposed by Hegde and others is also necessary. We use the Fano's inequality on well constructed ensembles as our main tool in establishing information theoretic lower bounds.