Competitive Facility Location under Random Utilities and Routing Constraints

In this paper, we study a facility location problem within a competitive market context, where customer demand is predicted by a random utility choice model. Unlike prior research, which primarily focuses on simple constraints such as a cardinality constraint on the number of selected locations, we introduce routing constraints that necessitate the selection of locations in a manner that guarantees the existence of a tour visiting all chosen locations while adhering to a specified tour length upper bound. Such routing constraints find crucial applications in various real-world scenarios. The problem at hand features a non-linear objective function, resulting from the utilization of random utilities, together with complex routing constraints, making it computationally challenging. To tackle this problem, we explore three types of valid cuts, namely, outer-approximation and submodular cuts to handle the nonlinear objective function, as well as sub-tour elimination cuts to address the complex routing constraints. These lead to the development of two exact solution methods: a nested cutting plane and nested branch-and-cut algorithms, where these valid cuts are iteratively added to a master problem through two nested loops. We also prove that our nested cutting plane method always converges to optimality after a finite number of iterations. Furthermore, we develop a local search-based metaheuristic tailored for solving large-scale instances and show its pros and cons compared to exact methods. Extensive experiments are conducted on problem instances of varying sizes, demonstrating that our approach excels in terms of solution quality and computation time when compared to other baseline approaches.

Optimal Privacy Preserving in Wireless Federated Learning System over Mobile Edge Computing

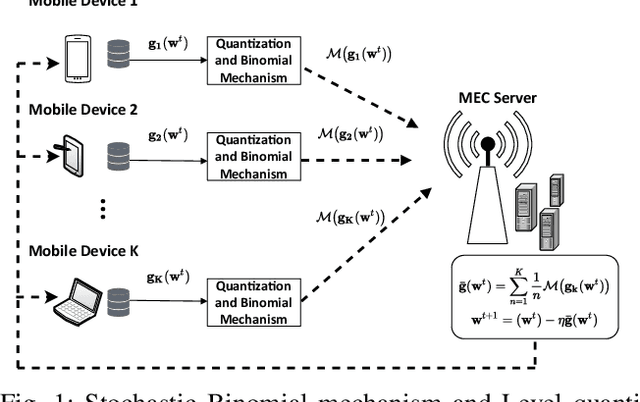
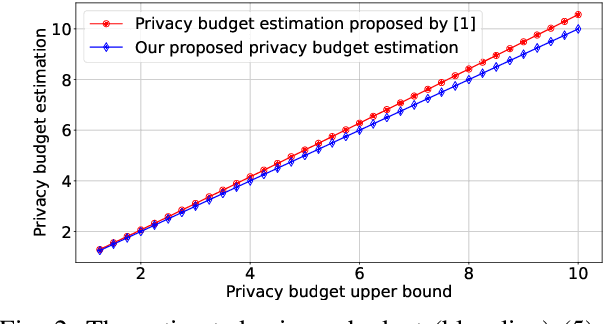
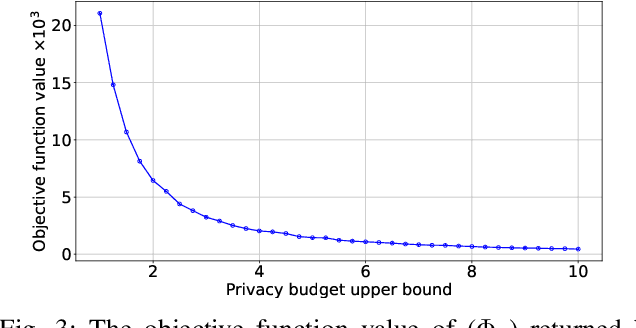
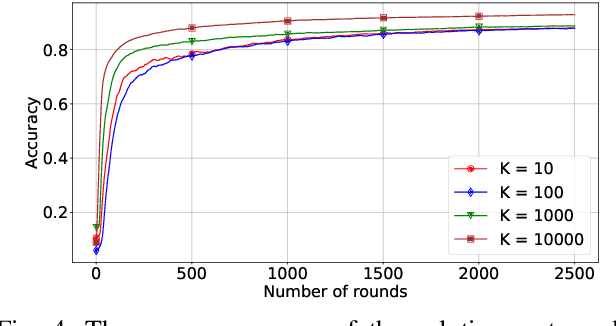
Federated Learning (FL) with quantization and deliberately added noise over wireless networks is a promising approach to preserve the user differential privacy while reducing the wireless resources. Specifically, an FL learning process can be fused with quantized Binomial mechanism-based updates contributed by multiple users to reduce the communication overhead/cost as well as to protect the privacy of {participating} users. However, the optimization of wireless transmission and quantization parameters (e.g., transmit power, bandwidth, and quantization bits) as well as the added noise while guaranteeing the privacy requirement and the performance of the learned FL model remains an open and challenging problem. In this paper, we aim to jointly optimize the level of quantization, parameters of the Binomial mechanism, and devices' transmit powers to minimize the training time under the constraints of the wireless networks. The resulting optimization turns out to be a Mixed Integer Non-linear Programming (MINLP) problem, which is known to be NP-hard. To tackle it, we transform this MINLP problem into a new problem whose solutions are proved to be the optimal solutions of the original one. We then propose an approximate algorithm that can solve the transformed problem with an arbitrary relative error guarantee. Intensive simulations show that for the same wireless resources the proposed approach achieves the highest accuracy, close to that of the standard FL with no quantization and no noise added. This suggests the faster convergence/training time of the proposed wireless FL framework while optimally preserving users' privacy.